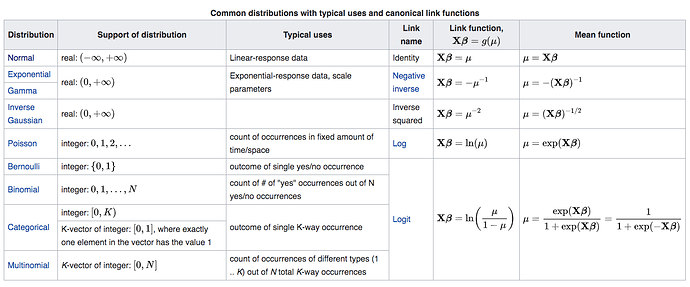
It seems that there are common pairs of the noise distribution (likelihood) and the link function (inverse of the nonlinearity) in the use of GLM. Why is it like that?
1 Like
It’s a very long story that involves exponential family distributions. Short answer is that the likelihood and link function have similar mathematical forms so they can be combined if you want to do analytical derivations of things like Maximum Likelihood or Maximum A Posteriori. These days however, you can use gradient descent and frameworks like PyTorch to fit any mathematical model you want, so we’re not really restricted any more to these particular combinations of noise distribution and link function. Just set up a Pytorch model and start training! (You’ll learn in week 3 how to do that).
3 Likes