Converting 4d (3d+t) BOLD image to 3d (2d+t) flat map?

, , ,
1

Hello, does anyone know how to convert a 4d (3d+time) BOLD image into a 3d (2d+time) flat map of BOLD activity? i have surfaces obtained through freesurfer, and i’m experimenting with SUMA in AFNI, but it seems to be mainly for visualizing single 3d maps (correlation maps, for example) as surfaces.

is there a way to get my raw BOLD 4d image into a 2d+Time flat map (Basically, a time series of flat maps)?

why do i want 2d+t flat maps? because i’m trying to experiment with some CNN for image decoding using FMRI…most approaches i’ve seen have simply stacked the voxels (ignoring spatial relationships between the voxels, and hence not able to use convolutional layers).

thanks!

1 Like
2

Do you mean splitting a (X, Y, Z, T) matrix into Z (X, Y, T) matrices? Or resampling to the cortical surface and projecting that onto a rectangular grid?

If the former, it’s quite easy (fslsplit -z). If the latter, I’ve found some papers but no software:

If something else, do you have a reference?

3

ideally, resampling to cortical surface and projecting that to a rectangular grid.

i’ll take a look at fslsplit, it might be a quick solution to what i need.

thanks for the resources :slight_smile:

edit - no, fsl split isn’t what i need, at all, from what i understand it just extracts 3d time points from the 4d image.

the surface representation is what i need, or i could just use 3d conv layers instead of 2d, probably won’t make much difference.

4

I don’t know of any published software that does this. https://www.math.fsu.edu/~mhurdal/research/flatmap.html seems to be quite research-y, and I don’t know what its outputs look like.

5

Hi-

You can use afni_proc.py to include projection onto your FreeSurfer-generated surface as part of your EPI+anatomical processing. This is done by including the “surf” block in afni_proc.py. Your final output stats from your GLM model are then surface dsets; these would give you your “2D+t” maps of EPIs on the surface (fitts* and errts* files), as well as your stats dset output on the surface.

Examples of this are included in the AFNI Bootcamp demos and lectures; you can see AFNI_data6/FT_analysis/s03.ap.surface, which is also Example 8 in the afni_proc.py help:
https://afni.nimh.nih.gov/pub/dist/doc/htmldoc/programs/afni_proc.py_sphx.html#example-8-surface-based-analysis

There is also a video lecture of teaching this in a Bootcamp here:
https://cbmm.mit.edu/afni
… with lectures 24-28 talking about SUMA usage in general, and lectures 26 (starting at about 29:00) through 28 talking about doing the surface projection with afni_proc.py explicitly.

In the AFNI Academy YouTube channel:


… a set of SUMA-related lectures will also be up soon.

–pt

6

thanks Paul, i’ll give this a try and let you know,

Russell

1 Like
8

@ptaylor, Didin’t get th idea of how afni could help to generate flat 2d grid representation of 3d fmri? As i get @Rbutler right he would like to get flat grid representation of fmri data. BTW I am looking for solution how to transform rfMRI_REST1_LR_Atlas_MSMAll_hp2000_clean.dtseries.nii to 2-d grid flat maps using spherical to cartesial coordinate transfrom to apply.

9

Hi, @Relyativist –

Minor note to start: “ADNI” is the Alzheimer’s Disease Neuroimaging Initiative, an data sharing iniative, while “AFNI” is an open source set of tools for MRI analyses; the latter was the subject of my earlier post. Much of the surface-based functionality in AFNI is a subset of tools called SUMA (SUrface MApping).

AFNI has tools for projecting volumetric data (e.g., NIFTI or BRIK/HEAD files) onto a surface (e.g., GITFI or other formats). One main program for this is 3dVol2Surf (and there is a complementary program for the reverse process, via 3dSurf2Vol). If you have gifti surfaces, we can discuss using those. Otherwise, a good place to get anatomical surfaces (such as the GM-WM boundary and pial surface) is FreeSurfer’s recon-all; after running that, you can convert its output into NIFTI+GIFTI (with the benefit that the GIFTI are on standard meshes) with AFNI’s @SUMA_Make_Spec_FS.

In the above query, I noted that this functionality can be tied in with FMRI processing using the main AFNI tool for setting up FMRI pipelines, afni_proc.py; the user includes some of the files that have been run through recon-all and @SUMA_Make_Spec _FS as inputs to the program, as well as the “surf” block, and the EPI data will be projected onto the anatomical surfaces.

Creating flat maps specifically-- not just projecting onto embedded anatomical surfaces-- is a bit more complicated. There are a few ways to do it, linked in this Message Board posting:
https://afni.nimh.nih.gov/afni/community/board/read.php?1,158211,158226#msg-158226

I’m not quite sure about using spherical projection for this; typically one would project onto an anatomical surface, and then maybe flatten that. Are you kind of treating the brain like a globe surface, to project onto a map, like a Mercator/etc. projection? Often, using the semi-inflated hemispheres is a nice way to view brain data, and that doesn’t involve projection, just some mesh operations.

–pt

10

@ptaylor, Thank you for pointing out my typo with ADNI, sure AFNI.

Yes I’m trying to found out how to project fmri activations/signals on freesurfer ?h.sphere files onto Mercator rectangular 2d grid with particular size.

This won’t work as it delivers “ragged” map. The only related solution I’ve found is the opposite operation in cart2sph.m. It seems that spherical coordinates should be encoded in 2d grid as sin(theta). Something related to this:
Screenshot 2020-11-24 at 21.30.18

11

Hi, @Relyativist–

Hmm, interesting, OK.

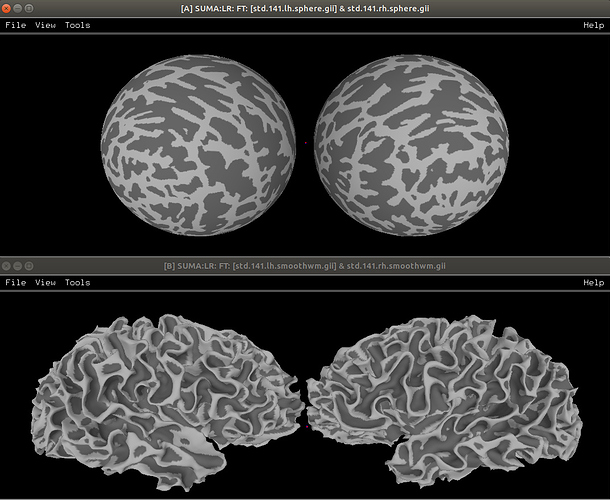
AFNI’s @SUMA_Make_Spec_FS translates a lot of FreeSurfer’s recon-all into standard format files; for example, surfaces can (should?) be converted to NIFTIs. This includes a sphere representation of each hemisphere, such as in the top panel here, which are topologically the same as the more anatomically correct lower panel surface hemispheres (viewed in SUMA):

suma_sphere_brain_imgs
suma_sphere_brain_imgs1075×880 224 KB

I guess the Mercator projection is just a formula for mapping points p_{\rm sph} = (\phi, \theta) on a unit sphere to a point on a rectangular grid p_{\rm rect}= (x, y). I guess I would approach this by dumping the points in the sphere (above), recentering them and normalizing them to a unit sphere; that gives you p_{{\rm sph}, i} for each $i$th node, and you could map that to p_{{\rm rect},i}. After that, you could map any node on that standard mesh to a point in your rectangular coordinates.

This command is an example of dumping each each node the coarser of the default standard meshes that @SUMA_Make_Spec_FS generates to mainly a text file (with some header info) that has 4 columns (node_index X Y Z):

SurfaceMetrics -coords -i_gii std.60.lh.sphere.gii -prefix std.60.lh.sphere

… which are stored in a new file called “std.60.lh.sphere.coord.1D.dset”, that can be dumped, without commented header info, into a new text file via, say:

1dcat std.60.lh.sphere.coord.coord.1D.dset > std.60.lh.sphere.coord.coord.dat

I was hoping I could find an existing program to scale this sphere, while keeping the same mesh, so the dumped points could be a unit sphere centered around the origin, but I haven’t found how to do that yet… at the moment, you could find the center of mass of the dumped coordinates, which will be a good estimate for the center, and shift that to the origin; then divide by the average distance to that new origin (which will be a good estimate of the radius). Then you would have your nodes all on a unit sphere, and be read to project away, while being able to project any other information at those same nodes in other corresponding meshes, too.

–pt

12

Hi @Rbutler,

Do you have any updates on this? I found out that someone used cart2sph.m, but its seems not ready-to-run solution.

13

Pycortex does that nicely

14

@Tommaso_p, could you please navigate how could rectangular maps could be recieved? as from example in Converting 4d (3d+t) BOLD image to 3d (2d+t) flat map? - #10 by Relyativist?