Downsample Image

, ,
1

Dear all,

I downsampled a mri image from 109,91,109 dimension to 65,77,65 with the AFNI command 3dresample.
It works fine for the change of dimension but it also slightly changes the overall size of the image and the position of the image.

Bildschirmfoto 2020-09-04 um 11.48.16
Bildschirmfoto 2020-09-04 um 11.48.163214×1148 288 KB

As you can see here, especially on the left hemisphere it does not fit anymore.
Do you know a way to avoid these changes?

2

Hi-

Can you please provide your exact 3dresample command?

And what is the output of the following for your original dataset DDD:
3dinfo -o3 -obliquity DDD
?

Also, what software are you using to visualize this here?

–pt

3

Thanks a lot for your reply.
command:
3dresample -input final_mask_wThalamus.nii.gz -prefix final_mask_wThalamus_2.82_2.82_2.82.nii.gz -dxyz 2.82 2.82 2.82

output:
** AFNI converts NIFTI_datatype=64 (FLOAT64) in file final_mask_wThalamus.nii.gz to FLOAT32
Warnings of this type will be muted for this session.
Set AFNI_NIFTI_TYPE_WARN to YES to see them all, NO to see none.
-90.000000 126.000000 -72.000000 0.000

I am using FSLeyes.

Thanks a lot!

4

Hi-

OK, thanks. Could you still please provide the output of this command on the data:
3dinfo -o3 -obliquity DDD
… so I can see the original resolution and if there is any obliquity present?

The 3dresample command shouldn’t change where the data appear in space; the only thing that will happen is the data will get a bit smoother (because all regridding processes lead to that). You can control the interpolation style with “-cmode”; there are also other ways to interpolate that might preserve edges better. Can I ask what the purpose of this resampling is-- such as, what kind of data set do you have, and why do you want it at the specified resolution? (There might be better ways to map your data, depending on this.)

I don’t actually know how fsleyes displays things. If you overlay these 2 images in the AFNI GUI, what does it look like?

–pt

5

Hi,

as mentioned above this is the output of 3dinfo -o3 -obliquity DDD

output:
** AFNI converts NIFTI_datatype=64 (FLOAT64) in file final_mask_wThalamus.nii.gz to FLOAT32
Warnings of this type will be muted for this session.
Set AFNI_NIFTI_TYPE_WARN to YES to see them all, NO to see none.
-90.000000 126.000000 -72.000000 0.000

So I am using the GSP Dataset and processed my data with fmriprep. fmriprep downsampled the GSP data to 65,77,65. So my mask (image I am downsampling with 3dresample) has to have to same dimensions.

Unfortunately, I cannot start the AFNI Gui on my Catalina MBO 2019 at the moment.

6

Howdy-

Wow, I’m not sure how I missed the output of your 3dinfo command in your earlier message… takes another sip of coffee. Sorry about that! And what’s worse, I actually provided the wrong option for what I wanted in 3dinfo… takes another sip of coffee. What is the output of this to show the original voxel size (I see there is no obliquity in that dset from the above command, but I also want to check to see if this is in original or a template space now):
3dinfo -ad3 -space DDD

I am not familiar with the GSP data, but I don’t see why it would be non-ordinary. 3dresample still shouldn’t be moving things around. In the image, your data doesn’t look like just a binary mask; but is that what you are ultimately going to apply this command to? (If so, one will want to use “-cmode NN” to have nearest-neighbor interpolation, to preserve binary masks.)

Would you be able to send me this dataset, so I can take a look at it?

Re. AFNI not working on your computer: that is a sad state of affairs, hopefully that should be fixable. Can I ask what the output of the AFNI system check on your computer is:

afni_system_check.py -check_all

?

–pt

7

Downsampling is treacherous due to aliasing effects. Schumacher’s seminal chapter General Filtered Image Rescaling describes this issue as well as providing one elegant solution. I think there are three solutions to this problem:

  1. blur data to Nyquist limit prior to downsampling
  2. use aliasing-aware FFT.
  3. adapt kernel width to compensate for aliasing (Schumacher’s approach).

I suggest you look at the links in this previous question. Specifically, AFNI’s 3dresample does not employ an anti-aliasing filter. You can see this by running the Python code below to generate a 3D zone plate. and then downsampling the resulting image using 3dresample:

3dresample -input zoneplate.nii -prefix cu -dxyz 2.844444444 2.844444444 2.844444444 -rmode Cu
3dresample -input zoneplate.nii -prefix li -dxyz 2.844444444 2.844444444 2.844444444 -rmode Li
3dresample -input zoneplate.nii -prefix nn -dxyz 2.844444444 2.844444444 2.844444444 -rmode NN

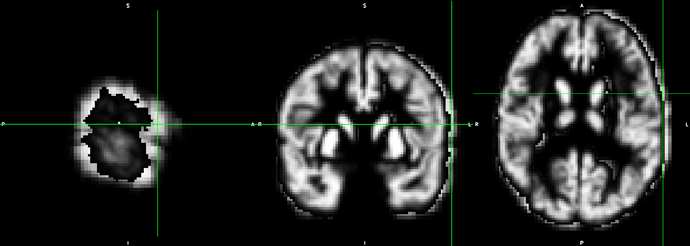
Below is the input image (left), 3dresample’s Cubic resampling (middle), and MRIcroGL’s Import/Tools/ResizeAndResample using anti-aliased Lanczos (right, using the method of Schumacher). The Matlab script nii_scale_dims would also anti-alias the data.

resize

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# python3 d_speed_size.py        : test speed/compression for folder 'corpus'
# python3 d_speed_size.py indir  : test speed/compression for folder 'indir'

import math
import numpy as np
import nibabel as nib

nvox = 128
print("Creating 3D zone plate of with {} rows/columns/slices".format(nvox))
img = np.zeros((nvox, nvox, nvox))
center = (img.shape[0]/2.,img.shape[1]/2.,img.shape[2]/2.)
grid_x, grid_y,grid_z  = np.mgrid[0:img.shape[0], 0:img.shape[1], 0:img.shape[2]]
grid_x = grid_x - center[0]
grid_y = grid_y - center[1]
grid_z = grid_z - center[2]
img = np.sqrt (np.square(grid_x) + np.square(grid_y) + np.square(grid_z))
img = np.reshape(img, (nvox, nvox, nvox))
header = nib.Nifti1Header()
affine = np.array([[1,0,0,-center[0]],[0,1,0,-center[1]],[0,0,1,-center[2]],[0,0,0,1] ])
nii = nib.Nifti1Image(img, affine, header)
nib.save(nii, 'distance.nii')
km = 0.7*math.pi
rm = max(center)
w = rm/10.0;
with np.nditer(img, op_flags=['readwrite']) as it:
    for vox in it:
        term1 = math.sin( (km * math.pow(vox,2)) / (2 * rm) )
        term2 = 0.5*np.tanh((rm - vox)/w) + 0.5;
        vox[...] = term1 * term2;
nii = nib.Nifti1Image(img, affine, header)
nib.save(nii, 'zoneplate.nii')
8

so for the original mask it says:
** AFNI converts NIFTI_datatype=64 (FLOAT64) in file final_mask_wThalamus.nii.gz to FLOAT32
Warnings of this type will be muted for this session.
Set AFNI_NIFTI_TYPE_WARN to YES to see them all, NO to see none.
2.000000 2.000000 2.000000 TLRC

Yes, I am going to make a mask out of that in python finally.

The GSP Dataset can be found here:
https://dataverse.harvard.edu/dataverse/GSP

afni system check ouput:
========================= summary, please fix: =========================

  • login shell ‘zsh’, trusting user to translate code examples from ‘tcsh’
  • shell zsh : MISSING env shell setup file .zshenv
  • have python version 3.7.6, some programs need 2.7.x
  • consider appending DYLD_LIBRARY_PATH with /opt/X11/lib/flat_namespace
9

Hi-

The Python comment is ignorable-- everything in AFNI is now Python3 compatible (except for one old bit of distributed MEICA code).
Do you still want to use zsh? That should still be OK. Could please copy+paste the following two lines to add this export command to your zsh startup file:

echo “” >> ~/.zshrc
echo “export DYLD_LIBRARY_PATH=${DYLD_LIBRARY_PATH}:/opt/X11/lib/flat_namespace” >> ~/.zshrc
… and if you open a new terminal, does typing “afni” or “suma” open up a GUI?

Which tarball in the set of GSP downloads contains your dataset? I searched for your filename, as well as “thalamus” but couldn’t find it specifically.

That voxel resampling doesn’t seem too steep, going from 2mm iso to 2.82 mm iso.

Note that in the end, you might want more than just the voxel size to match, having full grid matching. To do that, I would use the following to resample (note: “IDENTITY” is a keyword here, written as is; and I have fixed the formatting of this now, initially the backslashes weren’t there):

3dAllineate \
-input final_mask_wThalamus.nii.gz \
-1Dmatrix_apply IDENTITY \
-prefix final_mask_wThalamus_resampled.nii.gz \
-master [name of dset with relevant grid]

… and if you want to apply this to an integer-valued dataset, then to preserve that integer value, you can add the argument “-final NN”. For floating point dsets, using “-final wsinc5” will preserve edges the best (with a tiny bit of ringing added).

–pt

10

Two more points to make on this:

  1. If you are using 3dsample to match the grid of another dataset, use -master rather than -dxyz.
  2. Along the lines of Chris’s point, yes, you can slightly shift the data with this command, slightly (up to 1/2 voxel), because of using nearest neighbor interpolation (which is mostly necessary, since you are resampling a mask). The value at each output voxel is the value of the input voxel that has coordinates closest to those of the output voxel. That is NN interpolation. Since the output voxel coordinates (presumably) do not land on the centers of the input voxels, one mask voxel can have an apparent shift in coordinates.
    Consider a mask with a single voxel set, and a resample operation where the output voxels miss the set one by 1/2 voxel. Should that one voxel disappear? Should it be in the output dataset, but “move” by 1/2 voxel? If it should be in the output, which direction should it shift?
    These operations do not always have satisfactory solutions.
11

Thanks a lot for your reply @Chris_Rorden
I tried MRIcroGL’s Lanczos, but the resulting file seems to be a lot bigger than it was before.

Which of the 1.2.3. solution do you consider the best one?
And are there already implemented apps for anti-alias in python?

Best,

12

Thanks a lot! with 3dAllineate it seems to be the same result in the end.
-master would be my already downsampled image right?

13

Hi-

I would like to see the data set and try it out for myself. The download site you pointed to has a ton of datasets in tarballs to download, and I don’t know which is the correct one. Could you please be more specific about where this dataset exists? I could also send you a PM (personal message) about uploading the dsets in question, would I think would be the fastest way to go.

–pt

14

The GSP dataset is not the problem. It is the downsampling of the mask. And this mask can be generated in fsleyes with the atlas panel.

15

Hi-

I would still like to try visualizing+analyzing the actual dataset to see what is happening.

–pt