Estimating head/brain radius automatically

, , , ,
1

Are there any tools that can estimate head/brain radius from a brain mask or T1w image? Or, if this information is already calculated by FreeSurfer, that would work too.

2

If you have a brain mask, how about taking this relation:
V= (4/3) \pi r^3
ā€¦ and inverting it to get radius:
r= (3V/4\pi)^{1/3}
ā€¦ and then you just need the physical volume of the mask, which could be got, for example in AFNI:

3dROIstats -quiet -nomeanout -nzvolume -mask DSET_MASK DSET_MASK

? That should be a reasonable approximation.

ā€“pt

3

That is a great idea! Thanks!

4

For the record only as this a very SPM centric method.

If you have a gifti image of the pial surface, there is some code in there that can help here:

1 Like
5

Hi,

I got the following ideas using FSL and AFNI:

  • Use FSL bet on a T1w image with option -A : creates a mask with the edge of the inner skull mask: _inskull_mesh.nii.gz
  • Use fslstats to get the center of gravity of the image: fslstats T1w_brain.nii.gz -c (in mm coordinates)
  • use AFNIā€™s 3dmaskdump to get the coordinates of each non-zero voxel in the file : _inskull_mesh.nii.gz in a text file: 3dmaskdump -mask T1w_brain_inskull_mesh.nii.gz -xyz -o output.txt T1w.nii.gz
  • Compute the mean distance of cog with each non-zero voxel of _inskull_mesh.nii.gz:
    dist (in mm) = sqrt[(x1 -x2)^2 + (y1 - y2)^2 + (z1-z2)^2]
1 Like
6

I suspect it would be fun to estimate this way for many brains at many ages and see the distribution of brain radii estimates, especially to see how close they are to the common assumptions of 50mm in adults and 35mm in infants.

7

There are lots of ways to compute something ā€œradialishā€:

  1. Compute volume (per ptaylor) and approximate that volume as a sphere, so the radius is related to the cube root of the volume as in Paulā€™s formula above.

  2. Find distance from some kind of center to the edge of the brain (per jsein). This is equivalent or at least very similar of the center in the volume to every node on the outermost surface. Take the average of those edge distances or the minimum distance. Remi-Gauā€™s surface method computes distances across all voxels to the surface, so thatā€™s a little different.
    That center could be the center of mass, the deepest voxel (the ā€œpole of isolationā€). See this fun poster we did with Chris Rorden. https://afni.nimh.nih.gov/pub/dist/HBM2020/GlenEtal_FindingYourCenter_OHBM2020.pdf

  3. Find the bounding box for a relatively cardinalized (AC-PC or similar) dataset, and split the left-right distance in half.

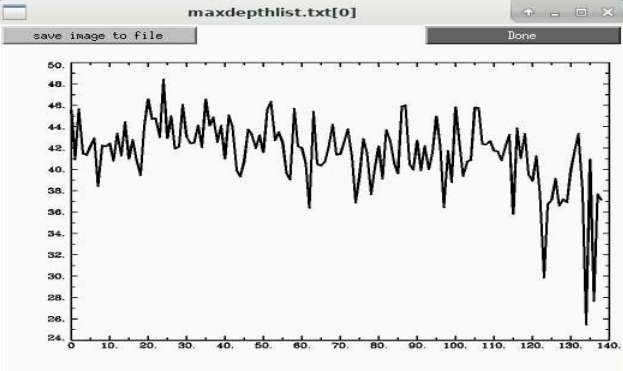
I tried the depth method using 3dDepthMap to find that deepest voxel for a variety of datasets with the simple script below and found a range of about 26-48mm for ages 8-78.

#!/bin/tcsh
# computing depth
set ddir = /data/NIMH_SSCC/p024_ds-frontiers-qc_REST/data_13_ssw

rm maxdepthlist.txt

foreach submask ( ${ddir}/sub-*/ses-01/mask_ss_cp.sub-*.nii )
   3dDepthMap -prefix depthskull.nii.gz -input $submask \
      -binary_only -zeros_are_zero -overwrite
   set maxdepth = `3dBrickStat -max -slow depthskull.nii.gz`
   echo $maxdepth $submask >> maxdepthlist.txt
   echo $maxdepth $submask 
end

That looks like this for 139 subjects we looked at recently across 7 sites:
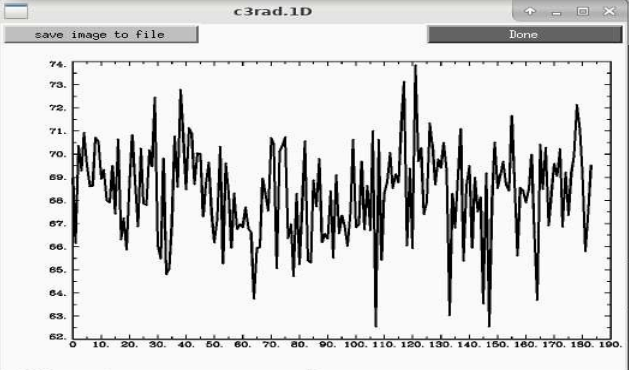
image

We actually used a variation of that volumetric->radius idea to control for dilation during averaging in this paper, A series of five populationā€specific Indian brain templates and atlases spanning ages 6ā€“60ā€‰years - PMC
Looking back at that data for the 18-25 year old group, that kind of radius varies from 65-75mm.
image

Mostly we donā€™t make too much assumption about 50mm that I know of with the only exception I can think of is how we compute the enorm time series. Those mix mm and degrees to give the Euclidean norm, and the assumption of 50mm gives almost exactly a 1 degree rotation from center of the dataset, making the scaling of degrees and mm similar. Itā€™s not critical though because thresholds are still somewhat arbitrary. That combination is less true for kids, and even less for most species.

3 Likes
8

It looks like this is how xcp_d as head_radius=auto:

From xcp_d GitHub: 298

Hereā€™s my proposal:

Add an auto option for the --head_radius parameter.
If auto, load the brain mask, count the number of non-zero voxels, and multiply that count by the > > voxel volume to get the brain volume in millimeters cubed.
Calculate the radius from the volume (radius = ((3 * volume) / (4 * np.pi)) ** (1 / 3)).

This is very cool; especially for large cross-sectional datasets focused on the lifespan!

However:

  • Is it problematic to assume that head-size radius is equal to approximate brain-size radius as described above?
  • Would it be an issue to use 50 mm (the default) when there are clear sex and age differences?
  • Also, brain size may have clinical significance in older populations (i.e., neurodegenerative disease). Any thoughts on that confound?

Thanks,
Bram

9

@bramdiamond The typical ā€œbrain radiusā€ or ā€œhead radiusā€ estimate for calculating framewise displacement (FD) is a placeholder for assuming the brain is approximated by a sphere. If anything, there is not exactly one brain radius in any brain unless it is treated like a sphere since brains are (usually) longer in the Anterior-Posterior axis and narrower in the Right-Left axis.

FD itself is an approximation of motion calculated by the sum of all displacements approximated in millimeters. It is not an absolute in that regard. Technically, to measure the actual magnitude of displacement in an MRI, you should only really need the affine matrix resulting from a rigid-body registration/normalization to calculate the single 3D vector of displacement (think back to physics or linear algebra vector magnitude calculation days, which I have not seen anyone ever try). FD is more conservative in approximating motion by ā€œover-valuingā€ every displacement (rotations and translations) in each of the 3 axes (X/Y/Z). So if someone makes a micro-movement in any axis, it will probably be an excluded/noisy fMRI frame.

2 Likes