Hi everyone!
I’m sorry I have a very general question, but I’m absolutely stuck and would appreciate any help.
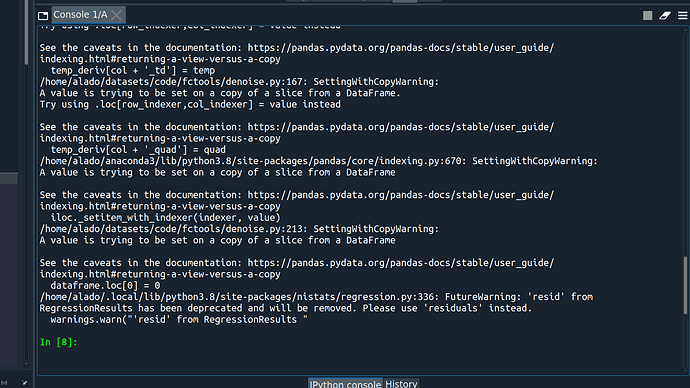
I’m trying to run a first-level analysis using nistats. But I keep getting only zeros and nans in r-squares, residual, and z-maps after computing contrasts.
Is there any mistake in my code that I can’t see?
glm = FirstLevelModel(
t_r=t_r,
hrf_model='glover',
drift_model='cosine',
#high_pass=0.01,
high_pass=0.008,
mask_img = fmri_mask, #nifti image
smoothing_fwhm=3.5,
noise_model='ar1',
standardize=False,
minimize_memory=False)
#fist level model
#events and confounds clean are data frames
glm = glm.fit(fmri_img, events=events, confounds=confounds_clean)
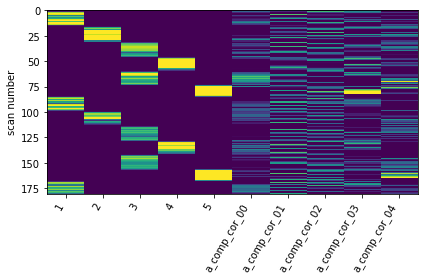
design_matrix = glm.design_matrices_[0]
#plot
ax = plot_design_matrix(design_matrix.iloc[:,0:10])
ax.get_images()[0].set_clim(0, 0.2)
#r`2: returns a list, take the first element, because we only have one run
r2_img = glm.r_square[0]
plotting.plot_stat_map(r2_img, threshold=0.2)
resids = glm.residuals[0]
n_columns = len(design_matrix.columns)
#10 contrasts
contrasts = {'0back-1back': np.pad([1, -1, 0, 0, 0], (0,n_columns-5)),
'0back-2back': np.pad([1, 0, -1, 0, 0], (0,n_columns-5)),
'0back-3back': np.pad([1, 0, 0, -1, 0], (0,n_columns-5)),
'0back-fix': np.pad([1, 0, 0, 0, -1], (0,n_columns-5)),
'1back-2back': np.pad([0, 1, -1, 0, 0], (0,n_columns-5)),
'1back-4back': np.pad([0, 1, 0, -1, 0], (0,n_columns-5)),
'1back-fix': np.pad([0, 1, 0, 0, -1], (0,n_columns-5)),
'2back-4back': np.pad([0, 0, 1, -1, 0], (0,n_columns-5)),
'2back-fix': np.pad([0, 0, 1, 0, -1], (0,n_columns-5)),
'4back-fix': np.pad([0, 0, 0, 1, -1], (0,n_columns-5))
}
for index, (contrast_id, contrast_val) in enumerate(contrasts.items()):
print('Contrast % 2i out of %i: %s' % (index + 1, len(contrasts), contrast_id))
# estimate the contasts
# note that the model implictly computes a fixed effect across the two sessions
#or here z_map = fmri_glm
z_map = glm.compute_contrast(contrast_val, output_type='z_score')
plotting.plot_stat_map(z_map)
I would appreciate any help or suggestions!