Hello Neurostars community,
I have a question about Bayesian inference on the group level.
First, a reduced description of the paradigm: 25 participants performed a 2-alternative force-choice task were they had to judge the amount of dots present on a floor and I fitted psychometric functions (PF) on the outcome with psignifit4, which uses Bayesian inference to estimate the parameters of the PF and directly provides credible intervals for these parameters. The one parameter I am interested in is the threshold (the point on the x-axis at which the PF intersects chance level performance of 0.5 on the y-axis).
There were 25 participants and each of them did the task with two conditions: (A) one with a higher amount of dots (e.g. 77) and (B) one with few dots (e.g. 33).
I would now like to know if the thresholds of condition A is actually higher than the one of condition B on the group level. Right now I am just taking the estimated thresholds of all 25 participants and two conditions and test with a t-test whether there is a significant difference between them. What bothers me is that I discard all the information that the posterior distribution of my Bayesian inference provides me about the certainty of the threshold (i.e. the credible intervals).
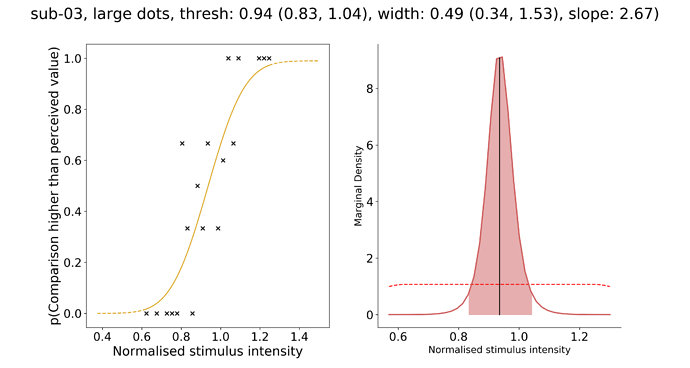
Below is an example fit of one participant and one condition. On the left subplot, you see the raw data (corsses) and the fitted PF, on the right subplot is the posterior distribution for the estimation of the threshold. The dotted line is the prior.
Does anyone know a good and easily accessible approach on group inference based on these obtained posterior distributions?
Thank you in advance and stay healthy!