I have a question about the multimodal simulations from the last part of today’s tutorial 1.
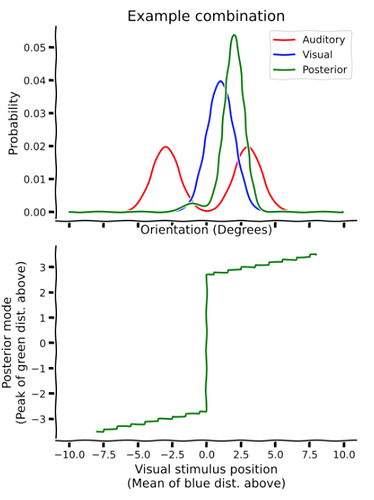
We had bimodal prior (peaks at -3 and 3) then the posterior mode (in the second plot) became greater less than 2.5 (soon greater than 3) or smaller than -2.5 (soon smaller than -3). This conflicts with my intuition where the posterior should be somewhere in the middle of two prior peaks, then converge to the peaks of the bimodal prior.
Why is this happening? Why does posterior become greater/smaller than two prior peaks?
The posterior is a function of likelihood an prior, posterior \propto likelihood \times prior. In the given example, the likelihood peaks closer to the right peak of the prior. So, the posterior is in between the right peak of the prior and the peak of the likelihood as expected. Given the specific sigmas for the distributions, the posterior can be lower/greater than the prior peaks. Recall also, that every time we normalize (after the multiplications).
So here, intuitively, given that the likelihood is closer to one of the two peaks, you have a very ‘strong’ posterior as the likelihood is also in this direction (you prior is 3, the likelihood is 2, so you have a high peak value at 2.5 -numbers are for illustration only).
Now, if you set the mean of the likelihood at zero, the posterior will be in the middle of the two peaks.
For this exercise, I think the bimodal prior should be visual and the likelihood should be auditory, i.e. we can see two people, and hear one sound. Then use posterior to estimate the real position of the sound. Is this right? Thanks!