Hello,
I am wondering if anyone can help me determine the best method to use in NiLearn.
I have a block design where participants did a four minute resting state scan and another separate four minute scan where they listen to white noise. All I am interested in doing is a Noise - Rest contrast, but I am wondering the best way to handle this in NiLearn given that they are in different runs.
Should I be concatenating the blocks and design matrices into a single run:
combined_bold = image.concat_imgs([noise_bold, rest_bold])
combined_design_matrix = pd.concat([design_matrix_noise, design_matrix_rest], axis=0, ignore_index=True)
Or should I be keeping them as separate runs:
combined_bold = [noise_bold, rest_bold]
combined_design_matrix = [design_matrix_noise, design_matrix_rest]
Much of the documentation on NiLearn shows multiple runs that also include multiple conditions. So, my only concern with the second option is whether there will be any contrast run given that there is only one condition in each run.
Subsequently, how should I handle this in the FirstLevelModel?
I am open to all suggestions and if there is a better course of action, please let me know.
Not sure I follow what your design is.
-
each of your run is 4 minutes long?
-
you have runs of resting state where the subject did nothing? So why do you call them block design?
-
you have runs where subjects listened to white noise? Do you mean for the whole 4 minutes of the run or for blocks of a certain duration interspersed with times where they listened to nothing?
Thanks for your response Remi. Allow me to clarify.
I have two separate runs - a resting state scan and a noise scan where participants listen to white noise. Each run had one single condition, so to answer your question, they listened to white noise for the entire 4 minute duration.
In hindsight, it would have been better to have a single run with white noise and rest interspersed, as you mentioned.
yup
a general rule of design efficiency is " Do not contrast trials that are far apart in time."
(see DesignEfficiency - MRC CBU Imaging Wiki)
it gets even worse when contrasting different conditions in different runs especially in this case where a run is just rest, you may a bunch of unknown confounds not only because of bio-physical / stats reason, but also because of psycho-cognitive reasons: so whatever results you get from analysis of this data, it should be taken with not just pinch of salt but probably a couple of handful of it!
actually if your noise run, do not have a single “rest” I am not even sure you can actually run your analysis, because you won’t have an “implicit baseline” to compare the activation of noise to…
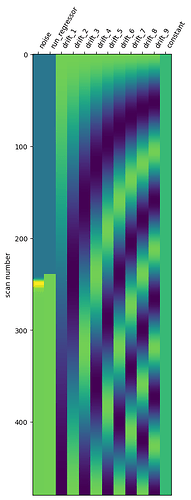
trying to explain that with code where I create a concatenated design matrix for both runs
when doing things this way, you may want to add a regressor to keep track of runs (which volume belongs to which run)
the problem is that in your case this regressor will be almost completely colinear with your regressor of interest (look at the 2 first regressors of the generated design matrix).
import numpy as np
import pandas as pd
from nilearn.plotting import plot_design_matrix
from nilearn.glm.first_level import make_first_level_design_matrix
t_r = 1
# 2 runs of 4 minutes
n_scans = 2 * 4 * 60
frame_times = (
np.arange(n_scans) * t_r
)
conditions = ["noise"]
duration = [4 * 60]
onsets = [4 * 60]
events = pd.DataFrame(
{"trial_type": conditions, "onset": onsets, "duration": duration}
)
# we need a regressor to keep track of what volume belong to which run
add_regs = np.vstack([np.zeros((4 * 60, 1)), np.ones((4 * 60, 1))] )
add_reg_names = ["run_regressor"]
X1 = make_first_level_design_matrix(
frame_times,
events,
add_regs=add_regs,
add_reg_names=add_reg_names,
)
plot_design_matrix(X1)
Right. This is what I suspected would be the case. So you suspect that there is nothing that I can do here?
Thanks for your help here.
I am not 100% sure there is nothing you can do, but I am not optmistic.
Would be curious to get second opinions on this though.
