Hello,
While a 2017 paper comprehensively addresses this topic in neuroimaging (ref below), I’m still a bit confused about specific terminology of testing/training/validation sets–and the concept of nested cross validation. Maybe my confusion is shared among others (or not!  ).
).
@GaelVaroquaux, @raamana , Engemann DA, Hoyos-Idrobo A, Schwartz Y, @bthirion (2017): Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines. Neuroimage 145:166–179.
Specifically, regarding the following figures:
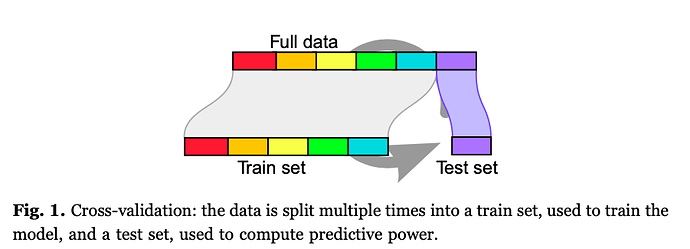
I understand the workflow of Figure 1. For example, here an SVM performance can be taken as the average accuracy on the test set of a 6-fold split (average of 6 accuracy measurements). The downside here is that “the amount of regularization becomes a parameter adjusted on data”.
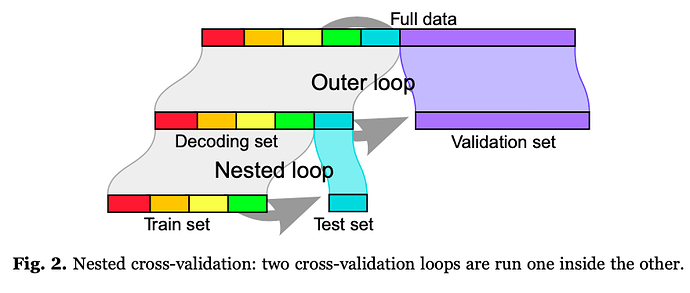
However, in Fig. 2, I’m not entirely sure how model performance would be assessed. According to the paper “the data are repeatedly split in a validation set and a decoding set to perform decoding. The decoding set itself is split in multiple train and test sets with the same validation set, forming an inner “nested” cross-validation loop used to set the regularization hyper-parameter, while the external loop varying the validation set is used to measure prediction performance”.
Is the idea here to take the SVM model with the maximum accuracy across the 5-folds (in the nested loop), and to test it (ignoring the four others) on the validation loop? Also, is there a standard number of times or data volume to split the data in “validation sets”? Would the model performance be the average across those multiple validation sets accuracies?
Apologies if this is specifically stated elsewhere in the paper.
Many thanks,
Tom
1 Like
Hi @tomvanasse,
This conceptual understanding of nested CV is often an issue with new ML practitioners so it’s great that you raise this question.
I will will answer here very briefly and pragmatically:
The first aim is to estimate the “generalization performance” given a limited amount of data. So the inner CV loops are used for parameter tuning and the outer loops for actually estimating the performance. So basically you should use the average accuracy over the outer loops as your generalization estimate.
The second aim is to get a “final model” that you can apply to completely new data where the labels/target is not known. Here again there two possibilities, either you perform another CV on the “complete data” to estimate the hyperparameters or alternatively use some aggregation over the hyperparameters from your previous CV runs you used estimate the generalization error to train the final model. I am not aware of any systematic comparison between these two but if you or someone else knows any references that will be a great addition here.
Kinda in a different direction but have a look at the answer here which can be illumination.
I will also shamelessly advertise our package julearn which puts a thin layer over scikit-learn to make CV easier.
I hope that this helps.
Best regards,
Kaustubh
2 Likes
Thanks @kpatil for your reply, it definitely helps. I haven’t really adjusted the different svc kernels/tuning parameters yet from default sklearn settings (which may be incredibly naive!).
In preparation for applying a classifier to my dataset, would it be a good idea to “lock-box” a partition of my sample which would serve as “out-of-sample” (15%=160 samples) to test a final model performance (which I won’t look at until the very end)? Also, Is the julearn package able to handle “group k-folds”? I believe I need to separate my k-folds by relevant blocks (subjects ids).
Thanks,
Tom
Is the idea here to take the SVM model with the maximum accuracy across the 5-folds (in the nested loop), and to test it (ignoring the four others) on the validation loop?
Actually, there are 2 possibilities. If you consider that the inner loop was only to learn some hyperparameter, you retain the hyperparameter that maximizes the inner loop accuracy and use the hyperparameter to retrain the model on the full dataset.
Another possibility is to pick the model that outperformed in each fold and aggregate their output on the validation set.
Also, is there a standard number of times or data volume to split the data in “validation sets”?
The more, the better. Deterministic decompositions such as 5-fol may noot be optimal. I would recomment the ShuffleSplit approach that samples a random dataset with e.g. 25% of the data, and run it for 100 folds.
Would the model performance be the average across those multiple validation sets accuracies?
yes
HTH,
Bertrand
1 Like
Hi Tom,
Leaving some of the data as a hold-out test set is usually a good idea (if you can afford it). In this case you can compare your CV estimate with the hold-out test set accuracy. If those two are close to each other then it adds confidence to the model parameters that there “generalize”.
I am not exactly sure what you mean by “group k-fold” but in general if it’s supported by sk-learn then it can be used in julearn. If it’s not a feature of sk-learn then if you describe what you want to achieve then we can try to implement it in the next release.
Best regards,
Kaustubh
Thanks for the questions and answers, these were all helpful for me too!
1 Like
 ).
).