Hi gang,
I hope y’all are doing ok in these difficult times.
@jeromedockes and I had some “fun” endeavors running
a one-way repeated anova in nistats (still using the archived version, as the new release within nilearn is not here yet).
The design: I have 3 conditions and 23 participants. Based on that I want to investigate the effect of condition, that is the difference between the three levels of the factor condition, using a one-way repeated anova.
Here’s the design matrix:
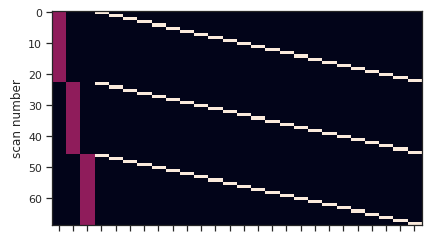
I set my contrast up as follows:
eoi = np.vstack(([1, 0, -1] + [0] * n_subjects, [0, 1, -1] + [0] * n_subjects, [1, 0, -1] + [0] * n_subjects))
which results in:
plot_contrast_matrix(eoi, second_level_design)

Looks ok, but running the model results in the following error:
second_level_model.compute_contrast(
eoi,
second_level_stat_type='F',
output_type='z_score')
LinAlgError: Singular matrix (here)
Does anyone have any idea what might go wrong (anyone as in @bthirion maybe)?
Cheers, Peer
Based on this nistats example we saw I believe the second-level contrast should be
1 0 0 0 ... 0
0 1 0 0 ... 0
0 0 1 0 ... 0
(3 rows, 3 + n_subjects columns). but the docstrings of FirstLevelModel and SecondLevelModel give no information about 2-dimensional contrast vectors (for “F” stat type, as used in the example)
Yes, the matrix singular because the participants columns sum to 1, as do the conditions columns.
2 possibilities:
- remove the column of one participant
- remove the column of one condition (assuming that this is a baseline). Implicitly the other columns will represent a condition vs this baseline.
Does that sound OK ?
or remove the third row of contrast matrix which is redundant (and thus makes the matrix singular)
Hi @bthirion and @jeromedockes,
thx for the pointers. I decided to go with @jeromedockes suggestion, as we discussed that the effect of interest described here refers to testing condition 1 = condition 2 = condition 3 = 0 and the using only the first two rows to condition 1 = condition 2 = condition 3.
Thx again, cheers, Peer

