Hello! I’ve got troubles in figuring out, why do we use np.finfo(float).eps when defining my_Bayes_model_mse in Tutorial 3, W2D1. It followed by a hint note: " # Hint: use ‘np.finfo(float).eps’ to avoid overflow", but I can’t understand, how it works. Could I ask for help with this?
That line says “give me the smallest possible positive number that the float datatype can represent on my machine”. In the context of the solution code, it’s being used to avoiding taking the log of 0 while still representing an asymptotically small likelihood.
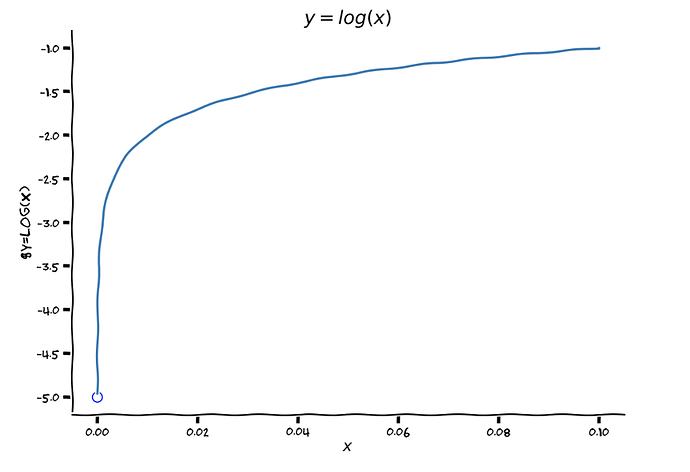
Here’s a plot of y=log(x) near zero
Do you see what’s happening here as log(x) approaches zero from the right? Its value is certainly not 5!
Another way to think about it is from the definition of logarithm: If log_10(X) = Y, then X=10^Y. To calculate log(0), we need to find a number such that 10^Y = 0. Let’s try 0: 10^0 = 1, which is no good. 10^-1 = 0.1 (a bit better), 10^-2 = 0.01 (closer) 10^-3 = 0.001, 10^-4 = 0.0001. If you continue this pattens for a bit, it should become obvious that you can’t take the log of zero–the result would have to be infinitely small.
In fact if you try np.log10(0), you’ll find that the result is -inf. Infinities mess up all kinds of computation, so we’re going to replace an infinitely small number with…a very small one. np.finfo(float).eps returns “machine epsilon.” On most modern computers using 64 bit floats, this is 2^-52, or 2.22e-16. This odd value comes from how floating point numbers are stored, but for practical purposes, you can treat it as “vey nearly but not quite zero.” If you add it to your probabilities (which may include zero), you can then flip back and forth between likelihood and log likelihood without running into infinities.
np.finfo docs: https://numpy.org/doc/stable/reference/generated/numpy.finfo.html