Hi,
I recently started to analyse longitudinal data in cat12, which works great, as the manual is really helpful. I have 50 patients with two measurement points (6 months apart), and their respective symptom severity at both measurement timepoints.
Now, I was wondering if it is possible to run something like a regression analysis in cat12/spm12, something along the lines of “changes in symptom severity ~ changes in brain structure”, so if e.g. if an improvement in symptom severity would also be reflected by structural brain changes.
I am rather lost with the contrast, and I was wondering if anyone here can double check/confirm if things were done properly?
My design matrix looks as follows (see below in image): Column 1 and 2 represent the images (one group only) with the two different timepoints (column 1 = timepoint 1, column 2 = timepoint 2). Column 3 and 4 are symptom severity at timepoint 1 and 2. This, I prepared according to the CAT12 manual, which was very straight forward (Flexible factorial model).
Regarding the contrasts, I found some examples on how to do regression analyses in cat12/spm for cross-sectional data with two groups, and tried to adapt it for my longitudinal data with one group. And I got the following “possible” contrasts:
% Contrasts
matlabbatch{4}.spm.stats.con.spmmat(1) = cfg_dep('Model estimation: SPM.mat File', substruct('.','val', '{}',{3}, '.','val', '{}',{1}, '.','val', '{}',{1}), substruct('.','spmmat'));
matlabbatch{4}.spm.stats.con.consess{1}.tcon.name = 'T1 > FUP';
matlabbatch{4}.spm.stats.con.consess{1}.tcon.weights = [1 -1];
matlabbatch{4}.spm.stats.con.consess{1}.tcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{2}.tcon.name = 'T1 < FUP';
matlabbatch{4}.spm.stats.con.consess{2}.tcon.weights = [-1 1];
matlabbatch{4}.spm.stats.con.consess{2}.tcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{3}.fcon.name = 'Any difference in time';
matlabbatch{4}.spm.stats.con.consess{3}.fcon.weights = [0.5 -0.5
-0.5 0.5];
matlabbatch{4}.spm.stats.con.consess{3}.fcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{4}.tcon.name = 'Regression slope T1 > FUP';
matlabbatch{4}.spm.stats.con.consess{4}.tcon.weights = [0 0 1 -1];
matlabbatch{4}.spm.stats.con.consess{4}.tcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{5}.tcon.name = 'Regression slope T1 < FUP';
matlabbatch{4}.spm.stats.con.consess{5}.tcon.weights = [0 0 -1 1];
matlabbatch{4}.spm.stats.con.consess{5}.tcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{6}.fcon.name = 'Any differences in Regression slope';
matlabbatch{4}.spm.stats.con.consess{6}.fcon.weights = [0 0 1 -1];
matlabbatch{4}.spm.stats.con.consess{6}.fcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{7}.fcon.name = 'Effects of interest (for plotting)';
matlabbatch{4}.spm.stats.con.consess{7}.fcon.weights = [0 0 1 0
0 0 0 1];
matlabbatch{4}.spm.stats.con.consess{7}.tcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.consess{8}.fcon.name = 'Interaction effect';
matlabbatch{4}.spm.stats.con.consess{8}.fcon.weights = [zeros(2,2) eye(2)-1/2];
matlabbatch{4}.spm.stats.con.consess{8}.tcon.sessrep = 'none';
matlabbatch{4}.spm.stats.con.delete = 0;
I’m particularly interested whether 1. this is even correct (especially contrasts 4-8)?
and 2. how would this be interpreted?
So what does the a) “Any differences in Regression slope” and b) “Interaction effect” mean with regards to the results?
Is it correct to state that “changes in symptom severity across time” are associated with “changes in brain structure” in those regions that popped up in the glas brain?
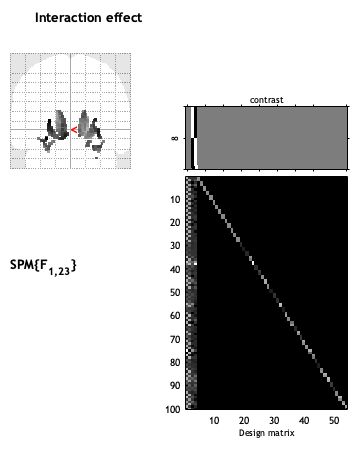
(Sorry, I would put more pictures of the contrasts, but I’m only allowed to upload one).
Hopefully, someone here can help me! Already a big thank in advance!