In Tutorial 2 ,
what is the L(θ | xi, yi) function like? I guess it is a normal distribution too.
While L(y | x, θ) normal distribution is very straightforward, how to get this second conditional probability equation?
In Tutorial 2 ,
what is the L(θ | xi, yi) function like? I guess it is a normal distribution too.
While L(y | x, θ) normal distribution is very straightforward, how to get this second conditional probability equation?
You can get from the second equation to the first via Bayes’ theorem. The likelihood of the data $p(\theta | x_i, y_i) \propto p(y_i| \theta, x_i) p(\theta)$. If you have that p(\theta) is a normal distribution (typical for ridge regression), and p(y_i| \theta, x_i) is a normal distribution (by assumption), then $p(\theta | x_i, y_i)$ is the product of two normal distributions, which is also a normal distribution (that’s one of the really nice properties of Gaussian distributions).
Ref: Bishop, Chapter 3, PRML [free pdf].
Thank you!
Bayes’ theorem is for switching a condition event with a target event. I am a bit confused by the three variables here.
I guess I will just keep “x” in condition still, and apply the Bayes’ equation for the other two variables:
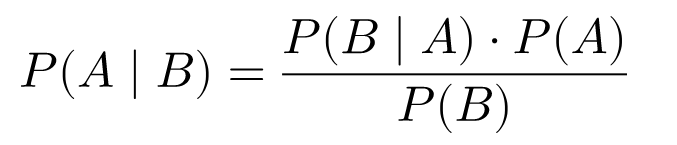
MANAGED BY INCF