Here is an equation from Video 1 defining the GLM. However, by directly transforming it to scalar form, \boldsymbol{\theta}^\top \boldsymbol{x}_t should equal to \sum_{i=0}^{d-1}{\theta_i x_i}. So can anyone help me understand why the x term is reversed? Thank you!
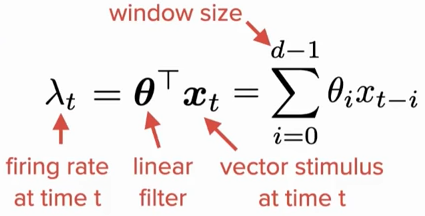
I might be wrong, but I think they present it like this to emphasize that you can think of the linear stage of a GLM as a discrete time convolution of the linear weights theta, which are similar to a filter, with the time varying input x: http://pilot.cnxproject.org/content/collection/col10064/latest/module/m10087/latest
In a convolution, you reverse one of the elements (typically the signal and not the filter but conv is symmetric so it doesn’t matter) and you slide it along. At each step you multiple the filter and signal and then sum them, then you advance one step t.
Hi Alex, thanks for your explanations! This is actually what I’ve always be confused by convolution/linear filter: if we define \theta in a way that y=\theta^\top x=\sum_{i}{\theta_i x_i}, then y would be larger when x is more “similar” to \theta. And this way it makes sense if we estimate \theta as the spike-triggered average \theta_{STA} or the MSE or MLE solution - we can interpret \theta as the optimal input that would trigger a spike. However, if we define \theta in a way that y=\theta * x=\sum_{i}{\theta_i x_{t-i}}, then I don’t really know how to interpret the \theta, and also the estimation of \theta should not be \theta_{STA} or (X^\top X)^{-1}X^\top y. So why would we want to make \theta a linear filter? Thanks!