Hey y’all, has anyone figured out in T1 Demo3 how to analytically get another pair of rewards that share the same value function? My brain is too exhausted to function at this point… 
Also in T1 Ex2, why in the solution they used
if reset: TDE_reset[state] = 0 else: TDE_reset[state] = reward + gamma * V[next_state] - V[state]
to reset the TD error for all trials instead of
if reset: TDE_reset[:, n] = np.zeros_like(TDE_reset[:, n]) else: TDE_reset[state, n] = reward + gamma * V[next_state] - V[state]
The take-home message from Section 3 might give you enough of a hint for the guessing game.
did you mean as long as the sum of the unit is 20, because the animal don’t care?
The thing that matters is the expected reward. The expected reward from (0.5 x 6) + (0.5 x 14) = 10. Any other pair with the same expectation should work. The same principle is at work with the probabilistic reward in the next section too.
Thanks for the hint, mate. I thought the question meant “the value function is the same for a reward of 6 and a reward of 14”, and ask me to find another pair that share the same value function… Now i get that the value function is calculated with either of them maybe the reward… Guess i need a nap…
Feedback from TA preparation:
Clarifications / Inconsistencies:
-
T1: In interactive demo 2, it’s impossible to truly set alpha to zero (ie no learning), even though the number 0.00 is shown (this is slightly confusing)
-
T1: In interactive demo 2: What is so special about states 9 and 19? Is at a position of a cue & of a reward? Maybe it would be better to explain it in the plot?
-
T2 section 2: maybe it will be less confusing to write q(a,s) = q(a) = … and comment that this environment does not change its state? Otherwise it is hard to relate it to the intro video.
-
T2: maybe add alpha=0.7 to plot_parameter_performance? It is not clear which epsilon is better in section 4.
Questions:
none reported.
From the Markov assumption to the first line, it’s just re-writing the value function as the expected sum of rewards, and then separating the first term of the sum from the rest.
From the first line to the second line, you need to take the expected value of r_{t+1} + gamma*V_pi(s_{t+1}). This expectation is computed over the distribution over actions (given by the policy \pi), and over the distribution over rewards and next-states (given by p(s’,r)).
In Section 1: TD-learning, Eq 2 is:
V(s_{t}) = \mathbb{E} [ G_{t} | s_{t}] = \mathbb{E} [r_{t+1} + \gamma V_{t+1} | s_{t}]
Should the V_{t+1} actually be V(s_{t+1})?
If not, can someone explain how they are related?
Yes, it should have been V(s_{t+1}). Nice catch!
I believe this is from the old version of T1. It was updated last night.
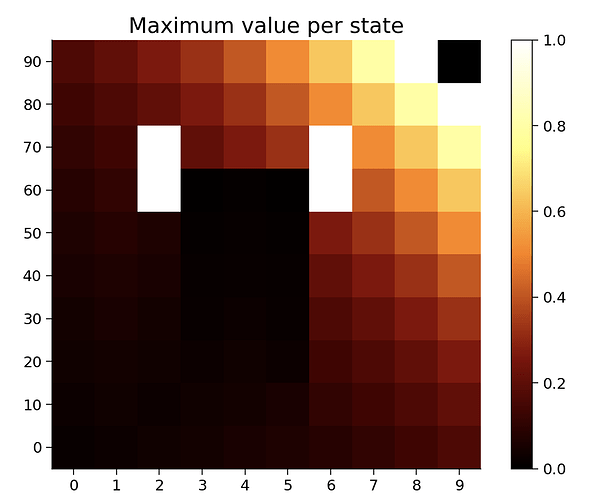
Let’s talk about what is being represented here:
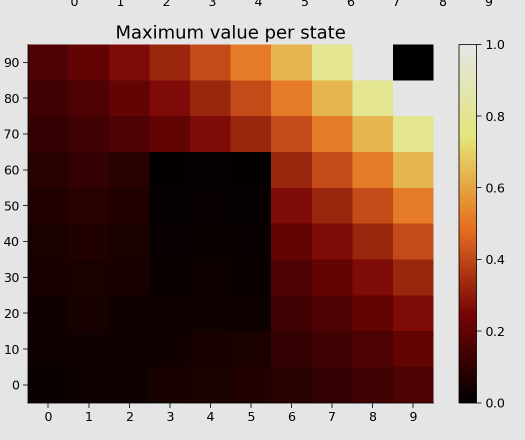
from Tutorial 4
That’s the value function: each square represents a state, and the color of the square represents the value of that state. The value is the expected sum of (discounted) future rewards. The range is between 0 and 1 because there’s a reward of 1 in the upper-right corner. Thus, the maximum value is one. The other values are <1 because the agent can access the reward from multiple routes, but longer routes lead to more discounting and, thus, values that are lower than one.