I am struggling to understand which is the best interpolation method to warp a functional image (for example an image which shows Cerebral Blood Flow) into its structural space. The methods which I tried are Linear Interpolation and Nearest Neighbor. The first one results into a smooth image, the latter into an image with sharper edges and clusters of definite different intensities. I was reading that the second method has the disadvantage to be “less accurate for non-linear data or when estimating values far from known points”. What does it mean “non-linear data” ? And “when estimating values far from known points” means that nearest neighbor algorithm could also assign values which is not the closest corresponding voxel in the source image ?
My problem is that my functional image has some NaN values. I should preserve as much as possible the position of such NaN values. For this reason, I tried Nearest Neighbor interpolation, besides the linear interpolation. However, I am a bit unhappy about the Nearest Neighbor general results as it seems to release a more uniform image with less variability. Can it be possible ? I expected the linear interpolation to release a smoother image and so with less variability among regions intensities.
Thanks in advance for any suggestion.
1 Like
I would suggest you look at the slide 183 and its neighbors in my imaging to inference course.
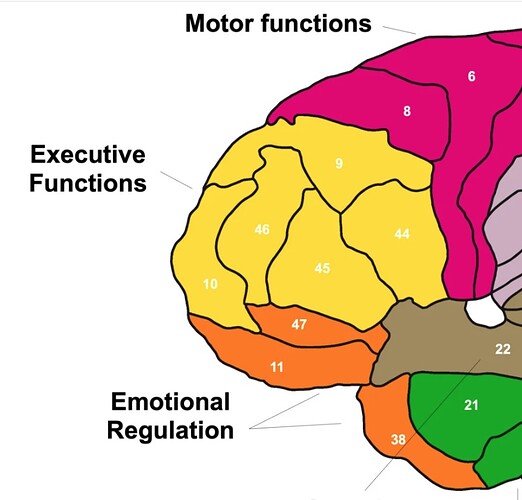
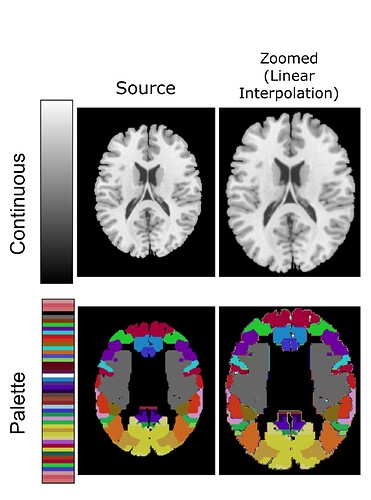
In general, I would only use nearest neighbor for indexed images, such as atlases. Consider a voxel that is composed 60% of area “45” and 40% of area “47”. It would not make sense to refer to this as either area “45.8” or area “46”. In this case, we would want to use nearest neighbor (or majority voting) to say that it is area 45.
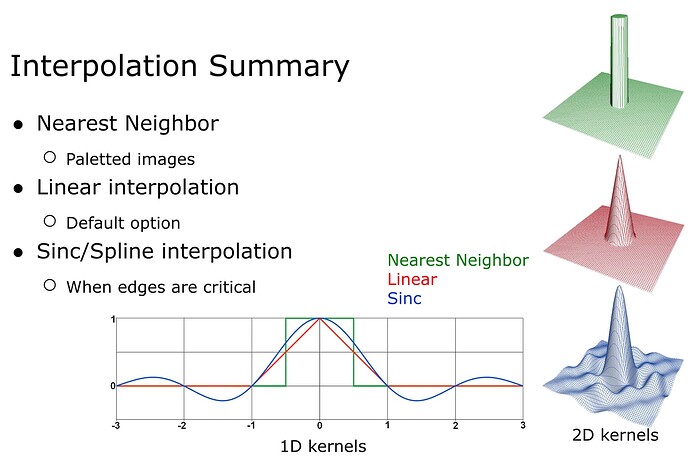
For scalar data such as your functional image, you will be much better served with linear interpolation, or perhaps even a higher order sinc/spline. This will preserve more of the high frequencies of your data.
In general, our field likes linear as it preserves more high frequencies than nearest neighbor but does not exhibit the ringing that can be seen with higher order interpolations.
I think you have to describe what the NaN values are supposed to represent? Are these voxels where you are unable to derive functions like time to peak or arterial input function? My sense is that the correct solution would be to warp your raw images into standard space first, and subsequently derive your CBF measures (with some voxels having NaNs). If this is really not possible, you will want to impute values for NaN voxels, warp the data to standard space with linear interpolation, shadow register you NaN mask (presumbably as a binary 1 and 0) to standard space with a nearest neighbor and re-insert the NaNs.
Sorry @neurolabusc I think you made a mistake here ?
True I corrected it. In general neuroimaging uses trilinear. While higher order filters preserve more high frequencies, they can cause ringing and are much slower to computer. Furthermore, we often apply smoothing to make the data a bit more normal, so higher frequencies would be lost.