Achieving (near) identical GLM t-statistics between FSL and nilearn

[flyingfalling]

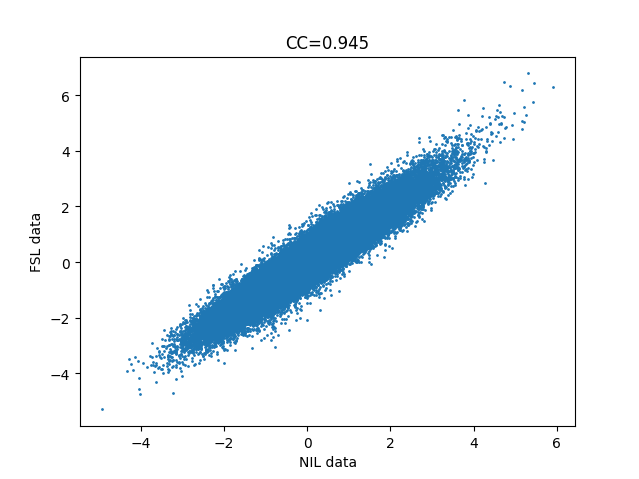
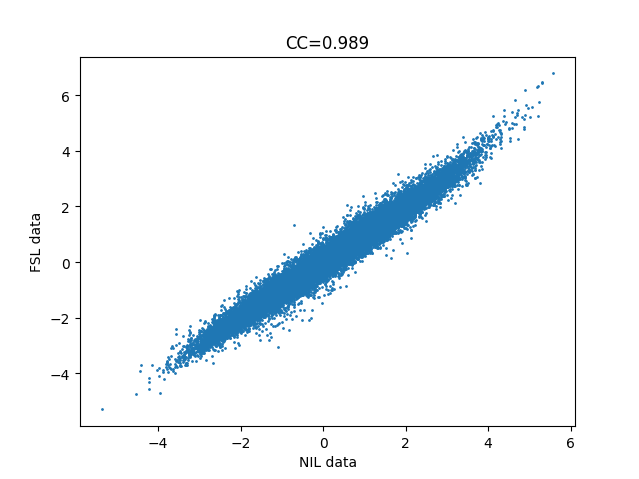
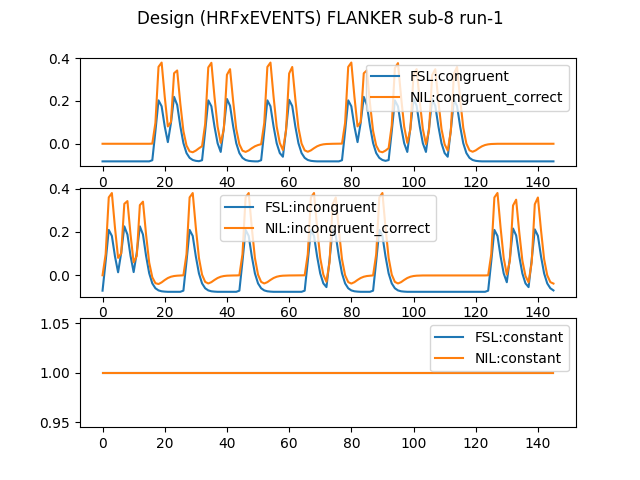
I’m attempting to demonstrate to students that identical analyses can be accomplished with different software. I’m trying to achieve (nearly identical) output from FEAT and nilearn, but am failing quite spectacularly (see attached image of correlation between t-statistic of all voxels of each, for the simple contrast of one condition).

I’m attaching the ‘best’ result I have been able to accomplish, which is a pearson’s r (CC) of 0.945. Considering this is simply the t-statistic of each voxel’s beta-weight for the given contrast (congruent), I am surprised, especially since the variance is symmetric for high and low t-statistic voxels.

Note the input data to both the NILEARN and FSL FEAT is identical BOLD volume series, precomputed by FMRIprep with default parameters. FMRIprep will have motion corrected but of course nuisance noise will still be present.

I expect the issue is that there are differen options versus built-in aspects in each software. One thing I suspect but can not confirm is that in the design matrix for NILEARN there is a “constant” (i.e. a bias term) column, which does not seem to be present in the design matrix of FSL, but it may simply not be showing it. I can not figure out how to get rid of it in NILEARN though.

I’m running a simple GLM in FSL FEAT (on the “flanker” task example from andysbrainbook: Chapter 5: Creating Timing Files — Andy's Brain Book 1.0 documentation).

This is just for run-1 of sub-8.

########## FEAT SETTINGS #########################
I disable EVERYTHING possible in FEAT:

MISC: Everything on the “misc” page is set to 0 (noise level, threshold, high pass filter, etc.) It is not clear whether this affects the GLM since it says it only relates to the efficiency calculation, but I have found it changes results sometimes.

DATA: High-pass filter cutoff is 0

STATS: Use FILM prewhitening is ON (This seems to by default apply an AR(1) model to the timecourse of each voxel, which it seems that NILEARN does by default as well. And since this can not be disabled in NILEARN I left it here in FEAT).
(FULL MODEL SETUP: 2 EVs, all options for the EV are disabled, I.e. add temporal derivative and apply temporal filtering are FALSE. This should not matter since we do not apply any temporal filtering to the BOLD signal).

POST-STATS: irrelevant, we already fail to achieve identical STATS (e.g. t-statistic) computed between NILEARN and FSL-FEAT. So the next step of clustering/thresholding will fail as well.

############# NILEARN SETTINGS ###################

mypath='/home/riveale/richard_home/git/fsl_tutorial_glm/fmriprep_results_flanker/sub-08/func/';
rawpath='/home/riveale/richard_home/git/fsl_tutorial_glm/raw_flanker/ds000102/sub-08/func/';
subject8_run1_f = os.path.join(mypath, 'sub-08_task-flanker_run-1_space-MNI152NLin2009cAsym_desc-preproc_bold.nii.gz');
subject8_run1_ev = os.path.join(rawpath, "sub-08_task-flanker_run-1_events.tsv");



df=pd.read_csv(subject8_run1_ev, sep = '\t');
## Exclude incorrect trials and only keep the three relevant columns as specified by NILEARN for building the regressors (predictors) matrix.

df = df[ df.correctness == 'correct' ];
df = df[ ['onset', "duration", "trial_type"] ];

glmparams=dict(t_r=2,
               slice_time_ref=0.5, #REV: fmriprep adjusts all slice times to the middle slice in each T_R.
               noise_model='ar1',
               standardize=False, 
               signal_scaling=False,  #REV: (0,1) is grand mean scaling, 0 is just normal, False is none.
               hrf_model="spm",
               drift_model=None,
               high_pass=0,
               verbose=3,
               mask_img=False, #Do not mask (default is None, which uses default data from BOLD img 4d volumes).
               );


fmri_glm = FirstLevelModel( **glmparams );
fmri_glm = fmri_glm.fit(subject8_run1_f, df); 
n_regressors = fmri_glm.design_matrices_[0].shape[1];
cong_contrast = np.zeros(n_regressors); 
cong_contrast[0] = 1; 
cong_z_map = fmri_glm.compute_contrast(cong_contrast, stat_type='t', output_type="z_score");
cong_z_map.to_filename("cong_raw_t_contrast_map.nii.gz")

[Remi-Gau]

There is an example in the nilearn doc that also compares FSL and nilearn output:

First level analysis of a complete BIDS dataset from openneuro

if you want to further reduce differences do like in the example: generate the design matrix with fsl and use it to fit the model with nilearn

but note that even when doing so you will have some differences in the output

[Remi-Gau]

Note similar past discussions: Nilearn vs. SPM very different results

See also Exploring the impact of analysis software on task fMRI results - PubMed

[flyingfalling]

@Remi-Gau Thank you for the insightful fast response and the HBM paper.

Indeed, I saw the tutorial in NILEARN that you linked. In fact it was one of my motivations for doing this demonstration…

The students and I were surprised that the correlation was not higher, since the solutions to the GLM equation are solved using well-established algorithms. I expected voxels with correspondingly larger t-statistics to be more “stable” between methods (i.e. not as affected by small changes in the values of the regressor/outcome), and thus was surprised that thresholding at high t-thresholds did not reliably produce identical maps (thinking naively that all the “noise” would be in low t-statistic voxels).

However, now that I think about it, this would not be the case, since each t-statistic would be directly related to the (estimated) null distribution of that voxel over time (or at least the sampling distribution, i.e. the standard error of BOLD values of that voxel). In a simple linear regression, increasing the variance by D, equivalent to moving one point roughly N*sqrt(D), will decrease the t-statistic by a factor proportional to sqrt(D)/sqrt(N), i.e. linear decrease by the amount that each data point moves…

I understand now what you mean by exporting the design matrix directly – you mean that the HRF-convolved predictor variables may be quite different than the one called “spm” in NILEARN. I agree this could have quite a large effect, so I will see how I can do this.

Best,
R

[flyingfalling]

I imported the HRF-convolved predictor used by FSL FEAT (as saved in design.mat), and achived a higher correlation, although still not as high as I would expect given the identical predictors now.

I am showing the different design matrices between FSL and NILEARN (presumably caused by different HRF functions or modifications thereof).

Note, I had to manually add a “constant” predictor to the two EV used by FSL to get the results.

[flyingfalling]

It would only let me put a single image in the post, so here is the comparison of the time series (predicted HRF based on task events) for FSL versus NILEARN.