Hi all!
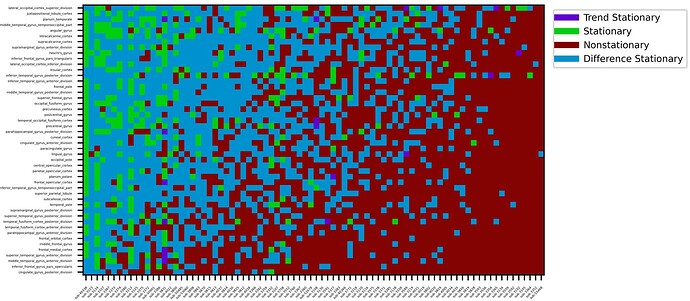
I am working on running Granger causality analysis on my dataset, and have run into a few problems that I’d like to clarify before I get too far ahead of myself. For the data, we have fMRI data that has undergone preprocessing with fmriprep. After this, the data were spatially smoothed (AFNI, 6mm kernel), scaled to global zero-mean (AFNI), and z-scored (ROI time-series are shifted to zero mean and scaled to unit variance). After this, I used the ADF and KPSS tests to test each ROI in each patient for stationarity (shown below). These decisions were made on the basis of this heuristic (source):
-
Both tests conclude that the series is not stationary - The series is not stationary
-
Both tests conclude that the series is stationary - The series is stationary
-
KPSS indicates stationarity and ADF indicates non-stationarity - The series is trend stationary. The trend needs to be removed to make the series strict stationary. The detrended series is checked for stationarity.
-
KPSS indicates non-stationarity and ADF indicates stationarity - The series is difference stationary. Differencing is to be used to make series stationary. The differenced series is checked for stationarity.
Here, ROI’s are shown on the y-axis, and patients are shown on the x-axis.
I am a bit confused on where I should go from here. I would like to be able to difference the Difference Stationary ROIs, but I would no longer be comparing the same data when I compare it to a region that has not been differenced. Additionally, I am wondering if there are more general preprocessing steps that I can perform without significantly influencing the data, as Granger Causality is quite sensitive to some preprocessing steps, especially those involving band-filtering, which is why I have been hesitant to use the confounds output by fmriprep, as these confounds are generated off of band-pass filtered data and are required to be used with a cosine filter.
I have already tried a couple of things, including cubature Kalman Filter-Smoothing, as described by Havlicek in 2011, but this did nothing to achieve stationarity, and all the p-values for ADF and KPSS were identical after running (I thought this was strange…).
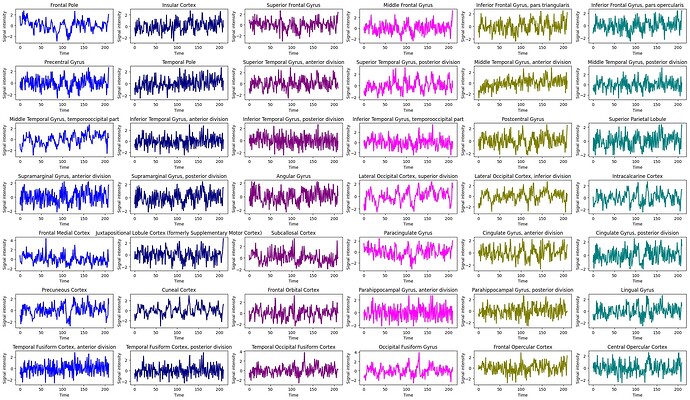
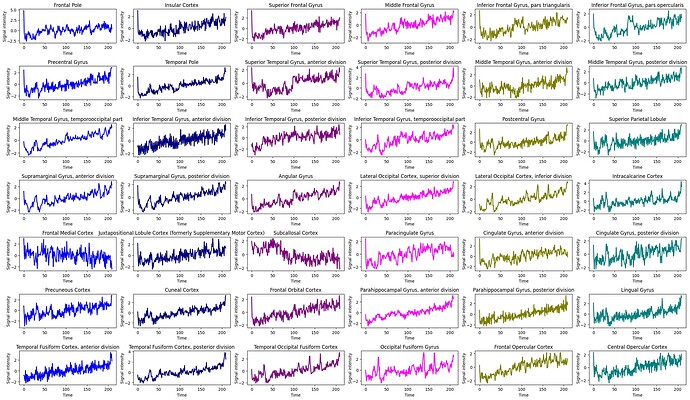
I have also attached a couple of images of time-series data from a patient with high stationarity and one with low stationarity:
High Stationarity
Low Stationarity
Ultimately, my query is how I can get these data to a sufficiently stationary state to be able to run GCA. If this is not possible, I have also considered using Toda-Yamamoto, but I am a bit unclear as to how this differs from GCA with respect to their assumptions surrounding cointegration.
Thank you all for your help and I am sorry for the long and scattered post!