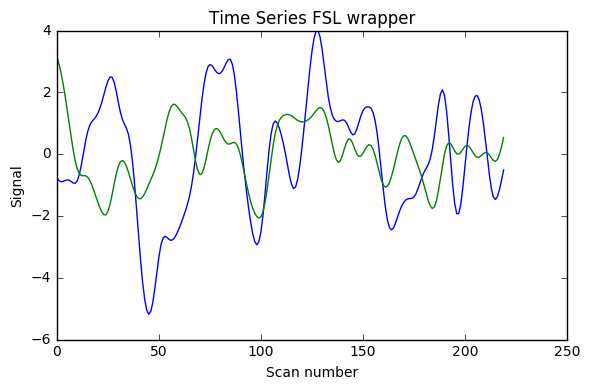
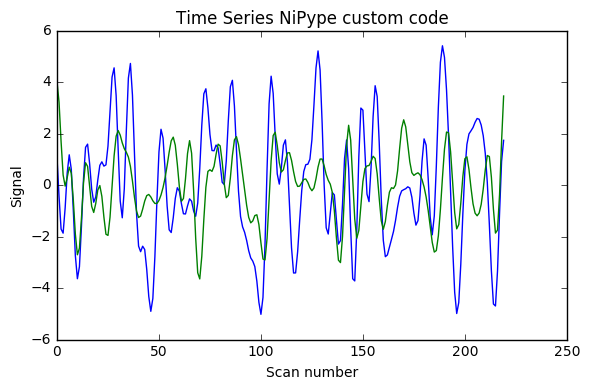
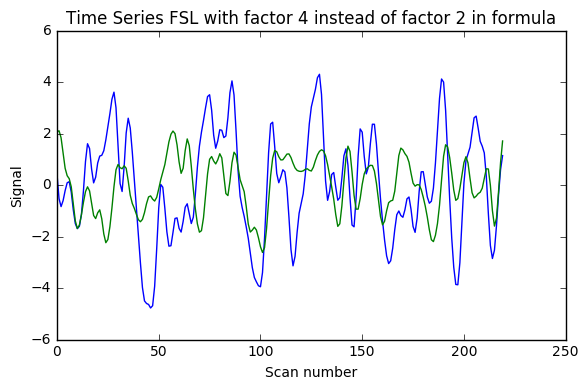
I implemented [0.008, 0.08] Hz band-pass filtering with both the FSL wrapper (with sigma = 1 / (2 * TR * cutoff_freq) as indicated here) and adapting for Python 3 the nipype code shown in this example (function bandpass_filter), using the code below. As can be seen in the image the results are very different (with what seems something like a factor 2 too much somewhere). Would anyone have suggestions why? (I double-checked that running the FSL command line gave the same results as the FSL wrapper below)
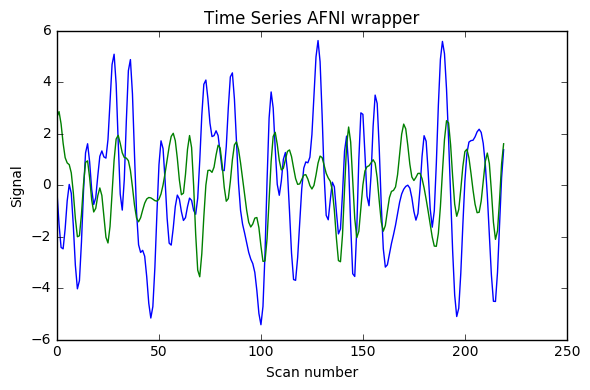
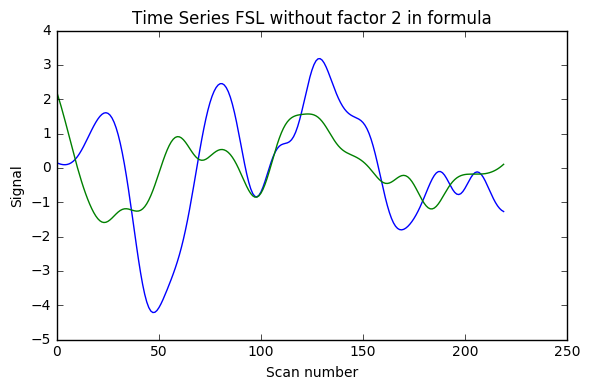
Update 1: I also added AFNI wrapper output which is very similar to nipype custom code, and FSL calculations without factor 2, and with factor 4 instead of 2.
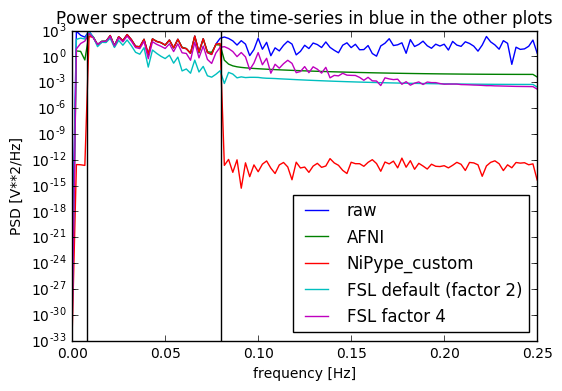
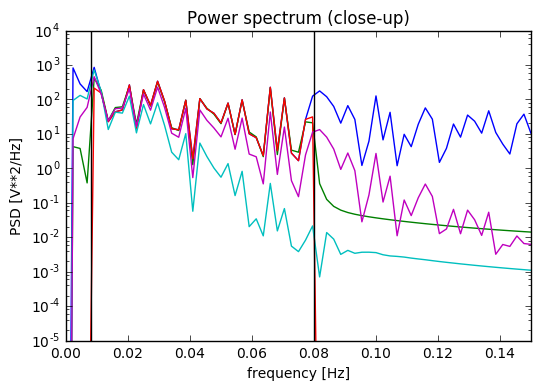
Update 2: I added at the very end a plot of the power spectrum of the time series, and it seems only NiPype custom function does what is intended.
HP_freq = 0.008
LP_freq = 0.08
### FSL
from nipype.interfaces.fsl import TemporalFilter
TF = TemporalFilter(in_file=in_file, out_file=out_file,
highpass_sigma = 1 / (2 * TR * HP_freq),
lowpass_sigma = 1 / (2 * TR * LP_freq))
TF.run()
### Nipype custom example
import os
import numpy as np
import nibabel as nb
sampling_rate = 1./TR
img = nb.load(in_file)
timepoints = img.shape[-1]
F = np.zeros((timepoints))
lowidx = timepoints // 2 + 1 # "/" replaced by "//"
if LP_freq > 0:
lowidx = int(np.round(LP_freq / sampling_rate * timepoints)) # "np.round(..." replaced by "int(np.round(..."
highidx = 0
if HP_freq > 0:
highidx = int(np.round(HP_freq / sampling_rate * timepoints)) # same
F[highidx:lowidx] = 1
F = ((F + F[::-1]) > 0).astype(int)
data = img.get_data()
if np.all(F == 1):
filtered_data = data
else:
filtered_data = np.real(np.fft.ifftn(np.fft.fftn(data) * F))
img_out = nb.Nifti1Image(filtered_data, img.get_affine(),
img.get_header())
img_out.to_filename(out_file)
### AFNI
from nipype.interfaces import afni
bandpass = afni.Bandpass(in_file=in_file, highpass=0.008, lowpass=0.08,
despike=False, no_detrend=True, notrans=True,
tr=2.0, out_file=out_file)
### FSL without factor 2 in formula
### FSL with factor 4 instead of factor 2 in formula