Dear Community,
I was asking myself if there would be differences between first-level results obtained by nilearn and SPM12. Therefore, I ran a very simple first-level analysis in both nilearn and SPM12. I used the same data as input for both methods, which in this case was smoothed functional MRI collected during a task in which subjects alternated between left-hand fingertapping and rest.
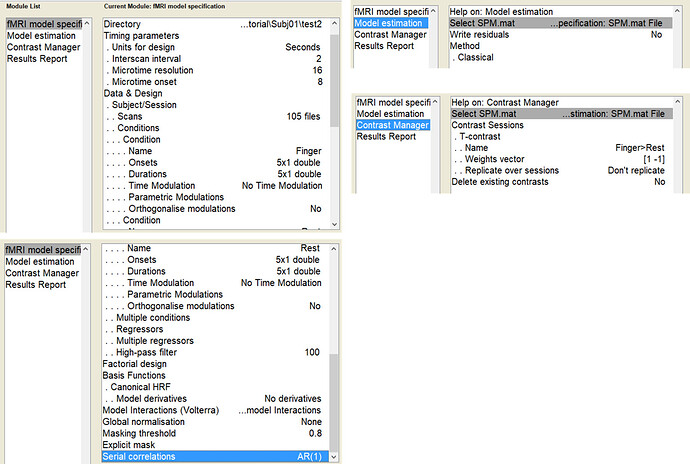
For the analysis, I tried to keep the same parameters in both methods, as much as possible. I used the same regressors of interest, slice time of reference, canonical HRF as provided by SPM, autoregressive model of first order, high-pass filter of 0.01 Hz. No first-level covariates were defined neither in nilearn nor SPM (to keep the computation as simple as possible).
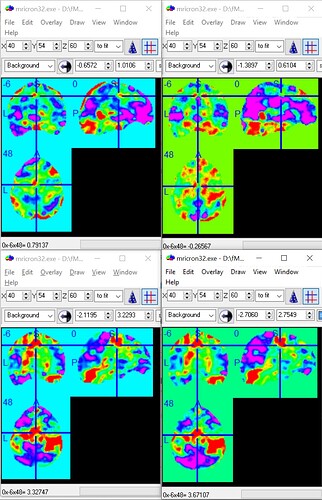
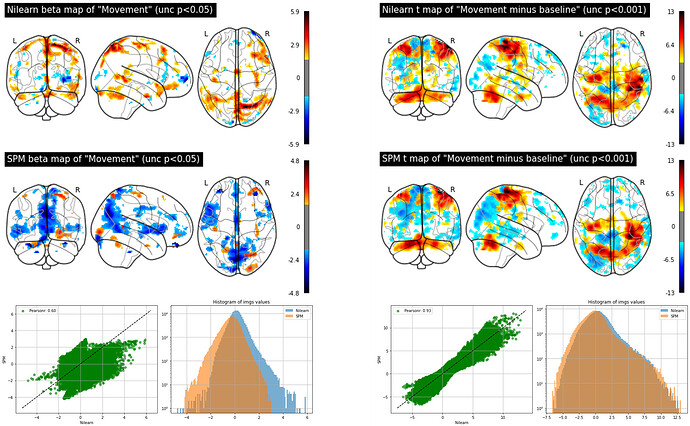
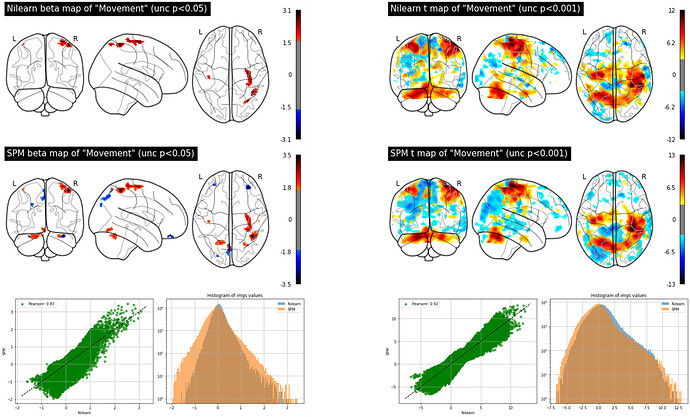
The figure below shows beta images for the regressor representing the finger tapping obtained by nilearn (top left) and SPM (top right). The figure also shows t-maps for the contrast finger-tapping minus rest obtained by nilearn (bottom left) and SPM (bottom right):
(Please find below the code I used to obtain the maps with nilearn and a screenshot of the SPM batch used)
So the conclusion is that both beta and t maps are different when obtained with nilearn or SPM and betas are more discrepant than t-maps. But one can also tell that the spatial patterns of the beta and t maps are similar by the way. First I was surprised about the results from nilearn and SPM being different, but I guess it’s also expected since there might be differences in the coding to compute the GLM in each method (SPM uses OLS to estimate the parameters and perhaps nilearn uses something else?)…
In any case, I’m asking myself what causes these differences between methods. Or maybe it’s something in my code/batch that is not exactly the same in both methods? (once again, please check those below) Following up, if my codes are not equivalent, how could I write them to perform the same computation? Finally, would those differences, if they are suppose to exist, raise a concern in terms of group analysis? (for example, one takes the betas in ROI analysis and I found the beta maps somewhat different from each other).
Many thanks for any input!
Best wishes,
Gustavo
########################
Script using nilearn for first-level analysis:
from sklearn.utils import Bunch
import pandas as pd
from nilearn.glm.first_level import FirstLevelModel
import numpy as np
from os.path import join
subject_data2 = Bunch(anat = 'D:\\fMRI analysis tutorial\\Subj01\\wanat.nii',
events = 'C:\\Users\\gsppa\\nilearn_data\\fMRI-motor-real-time\\sub-01\\func\\sub-01_task-motorRealTime_events.tsv',
func = 'C:\\Users\\gsppa\\nilearn_data\\fMRI-motor-real-time\\derivatives\\sub-01\\func\\sub-01_task-motorRealTime_desc-preproc_bold.nii'
)
events2 = pd.read_table(subject_data2["events"])
events2
fmri_glm2 = FirstLevelModel(
t_r=2,
slice_time_ref=0.5,
hrf_model='spm',
drift_model=None,
noise_model='ar1',
standardize=False,
high_pass=0.01,
)
fmri_glm2 = fmri_glm2.fit(subject_data2.func, events2)
conditions2 = {"movement": np.zeros(3), "rest": np.zeros(3)}
conditions2["movement"][0] = 1
conditions2["rest"][1] = 1
movement_only = conditions2["movement"]
outdir2='D:\\fMRI analysis tutorial\\Subj01\\test'
eff_map2 = fmri_glm2.compute_contrast(
movement_only, output_type='effect_size',
)
eff_map2.to_filename(join(outdir2, "movement_only_beta.nii"))
movement_minus_rest = conditions2["movement"]-conditions2["rest"]
eff_map3 = fmri_glm2.compute_contrast(
movement_minus_rest, stat_type='t', output_type='stat',
)
eff_map3.to_filename(join(outdir2, "movement_minus_rest_tmap.nii"))