fMRI Group analysis (2nd-level) - Which 1st-level contrasts for which model?

,
1

Hi everyone,

How do you correctly setup a 2nd-level (group-level) model, if you have only one group?

The question is simple, but to be honest, I have some doubts in my own approach. Especially, because FSL and SPM seem to handle this differently.

So, let’s setup the scenario:

  • I have one group of 12 subjects

  • Each subject did 4 sessions (sessions are the same, i.e all sessions contain all conditions)

  • The subjects were exposed to stimuli of 6 different conditions:

    cond01: audio-visual stimuli of category 1
    cond02: audio-visual stimuli of category 2
    cond03: visual stimuli of category 3
    cond04: repetition of visual stimuli of category 1
    cond05: repetition of visual stimuli of category 2
    cond06: repetition of visual stimuli of category 3

-> Therefore I have a 2x3 design (repetition x category)

As much as I can see, there seem to be 3 approaches that are used in our community to do the statistics on the group level:

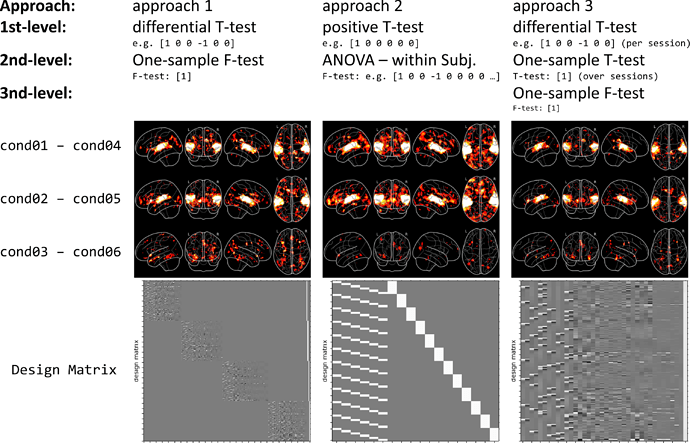
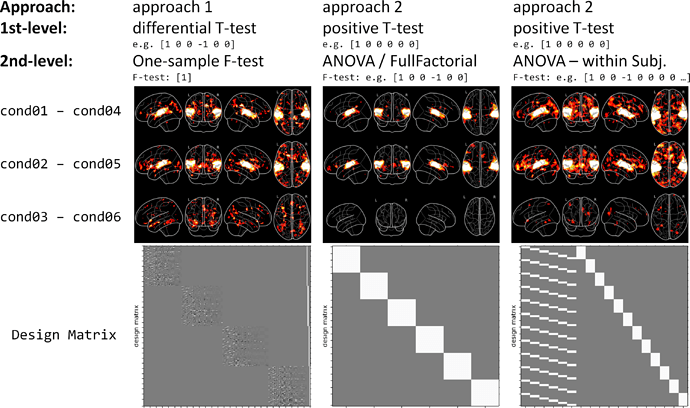
Approach 1: First, use all sessions for the 1st-level analysis and specify all contrasts of interests on this level. Second, perform a simple T or F-Test (group mean) on the 2nd-level.
Example: If I want to know which regions decrease in activation for the repetition of stimuli of category 1, I use a 1st-level differential T-contrast [1 0 0 -1 0 0] and a 2nd-level T-contrast [1].
Supported by: https://en.wikibooks.org/wiki/SPM/Group_Analysis, see line: “If this were a 2-by-2 design where both factors were within subject you would create four contrast images per subject: c1=[1 1 1 1], c2=[1 1 -1 -1], c3=[1 -1 1 -1], c4=[1 -1 -1 1] (overall effect, main effect 1, main effect 2, interaction). You would then create four second level designs, each being a one sample t-test…”

Approach 2: First, use all sessions for the 1st-level analysis and specify only “simple” positive contrasts on this level. Second, perform more “complex” differential contrasts (e.g. ANOVA, differential T-tests) on the 2nd-level.
Example: For the same question as above (effect of repetition of category 1), I would specify a T-contrast for cond01 [1 0 0 0 0 0] and one for cond03 [0 0 0 1 0 0] and than specify a 2nd-level contrast [1 -1].

Approach 3: First, conduct a 1st-level analysis for each session individually, with positive and/or differential contrasts on this level. Second, perform a 2nd-level analysis for each subject that computes the “global mean” of each contrast over all sessions. Third, perform a group analysis (3rd-level) analysis by computing the group mean with [1].
Example: This approach is mostly used by FSL (I think), as can be taken from this guide: https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/GLM#Multi-Session_.26_Multi-Subject_.28Repeated_Measures_-_Three_Level_Analysis.29

So this is my first problem: When should I chose which approach? Does this depend on the dependency between factors and on equal or unequal variance between them?

My second problem is about which group model to use. SPM gives me, amongst others, the option to perform a “One-way ANOVA”, a “One-way ANOVA – within subjects” or a “Full Factorial” design. And I’m not really sure which one to chose.

If I understand it correctly, than “One-way ANOVA - within subject” adds additional subject regressors, while “One-way ANOVA” and “Full Factorial” design seem to lead to the same Design Matrix. And all of them let me define if the factors are independent and if their variance are equal or unequal. Additionally, FSL seems to struggle with multiple contrasts on the group analysis (“https://www.youtube.com/watch?v=Ouc-3GOZWAo&t=9m10s”). Does this mean I shouldn’t use FSL for such a paradigm?

To better illustrate my problem, I’ve run a group analysis once with approach 1 and once with approach 2 (with “ANOVA” and “ANOVA – within subject” on the 2nd-level). The attached figure shows the different results (all group level contrasts were thresholded at voxel-level p < 0.005, no correction for multiple comparisons was applied).

question.png2994×1771 1.38 MB

And my third problem: I’m curious how others perform fMRI group analysis using Nipype. I only know how to create a pipeline for approach 1. What kind of pipeline do you use for your approach? Did somebody setup an FSL statistics pipeline that doesn’t need the FEAT output folders or the design.fsf file? i.e. is it possible to do statistics with FSL by just specifying a design matrix and using already preprocessed data? My guess is on the film_gls function.

I apologize for the wall of text. Any (even partial) answers, references to good reading materials or code snippets are highly appreciated.

Thanks,
Michael

2 Likes
2

Hi Michael!

I’ll do my best, but I’m not an expert SPM user. I do know what the design matrix should look like and am great with FSL!

I feel approaches 1 and 3 should be the same. Your results look roughly the same and some differences might occur because model 3 assumes the tasks are independent, but they might actually be correlated (meaning the level 1 regressors are correlated). Also, the residual variances will differ between the two models. At least from what I’m seeing here and based on what I know about SPM, I think they should be very similar.

Approach 2 is wrong. From what I can tell you’re not adjusting for repeated measures.

I think I answered the 2nd problem, correct?

Of course this doesn’t test your interaction. You didn’t ask, but I’ll tell you how :slight_smile: I’m going to use V1T1, V1T2, V2T1, V2T2, V3T1, V3T2 to describe your 3 conditions. Your F-test of interest is
V1T1-V1T2=V2T1-V2T2=V3T1-V3T2
to get the contrasts for SPM, do some algebra to get a 0 on the end. I’ll subtract V3T1-V3T2
V1T1-V1T2-V3T1+V3T2=V2T1-V2T2-V3T1+V3T2 = 0
So the two contrasts you’d specify and then select for your F-test for the interaction would be
V1T1-V1T2-V3T1+V3T2
and
V2T1-V2T2-V3T1+V3T2
Then if you find a significant interaction you can use either this same model or the first option to test what’s driving the interaction.

Hopefully that covers problems 1 and 2!

It is possible to run a group analysis in FSL without feat directories and it uses flameo. More here
http://blogs.warwick.ac.uk/nichols/entry/flame_without_1st/
I don’t know how to incorporate that into NiPype.

Hope that’s helpful.

Cheers,
Jeanette

2 Likes
3

Hi Jeanette,

Thank you very much for your answer. I actually went through all of your youtube videos to prepare for this topic. So, thank you also for those :slight_smile:

To clarify, the figure above only showed approach 1 and approach 2. But once approach 2 as a simple ANOVA (middle) and once as “ANOVA – within subject” (right). For completeness, I’ve also run approach 3 (in SPM) and updated the figure:

question02.png2994×1925 1.89 MB

Follow-up 1:
Is approach 2 wrong in general or just because I have repeated measures? SPM allows user to specify if conditions within factors are independent or not and if they have equal varinace or not. So by specifying that the factor “Repetition” is dependent and has equal variance, I would get a design matrix as follows:

Would that make approach 2 again legitimate?

Follow-up 2:
Thank you for your interaction example. Testing the interaction would be of course the next step. You have a good video that explains nicely how to setup such interaction contrasts in general (https://www.youtube.com/watch?v=pwU32mnID-I&t=9m49s), but I realized that your approach and the one that SPM sets up automatically differ “visually”.

Where yours is anchored to the last condition, the one from SPM is more like a “staircase”:

a1: 	1	0	0	-1				b1:	1	-1	 0	 0
a2: 	0	1	0	-1		and		b2:	0	 1	-1	 0
a3: 	0	0	1	-1				b3:	0	 0	 1	-1

Am I assuming correctly that they are actually the same? Because b1 = a1-a2 and b2 = a2-a3

Follow-up 3:
Independent of my approach: If I want to compute such an F-Test, do I perform it always on the 1st-level and use a simple One-sample T-test on the 2nd- and/or 3rd-level?

Bonus FSL Question:
Thank you for the link to Thomas Nichols’ flameo example. In the guide he mentions 4D COPE and 4D VARCOPE images. I’m not familiar with FSL’s terminology, but in this context, the 4D COPE files are the preprocessed functional images, correct? What would the 4D VARCOPE stand for?

Thank you again for your help.

Cheers,
Michael

4

Hi miykael,

Thanks for posting and explaining so well your question.

Sorry for reviving this thread, but I’d like to contribute in this discussion. It’s actually surprising that the topic is not so clear in our community.

Although less sensitive, obtaining first-level contrasts to be later taken to the second-level (your approach 1) is the easiest and the recommended way for SPM, at least in the case of a within-subjects design. This approach partitions the GLM error into separate components, which does not offer concerns about non-sphericity and controls false-positive results (when compared to pooled error).

Regarding repeated-measures design, one can then create 1st-level ANOVA contrasts for each run and average them in ImCalc (for SPM users). The one takes the averages to the 2nd-level contrast, which can be the mean across subjects.

For references, please refer to:

  • Henson R.N. (2015) Analysis of Variance (ANOVA). In: Arthur W. Toga, editor. Brain Mapping: An Encyclopedic Reference, vol. 1, pp. 477-481.
  • McFarquhar M. (2019). Modeling Group-Level Repeated Measurements of Neuroimaging Data Using the Univariate General Linear Model. Frontiers in Neuroscience, vol. 13.

Thanks to Guillaume Flandin for helping me to clarify this topic.

1 Like
5

Hi @miykael ,

I am a bit late to the game, but was wondering whether you were able to resolve how to model the group X treatment 2nd-level interaction in SPM via nipype?

For context, I have a 2 x 7 repeated-measures design. Factor A is a simple between-subject/group factor (liberals/conservatives) and Factor B are within-subject/exp. conditions (7 different trial categories).

On the 1st level, I have already conducted T-contrasts for every exp. condition vs. control, so I end up with 7 con_images per subject, for a total of 420 con_images (60 subjects total, 30 per group). I would now like to run a 2-LV analysis that captures the interaction between group X condition. I assume that the FactorialDesign is the appropriate class here, followed by EstimateModel and EstimateContrast.

My main questions are:

  1. how do I define the desired interaction contrast
  2. what would a potential nipype pipeline for this workflow look like?

Many thanks in advance!