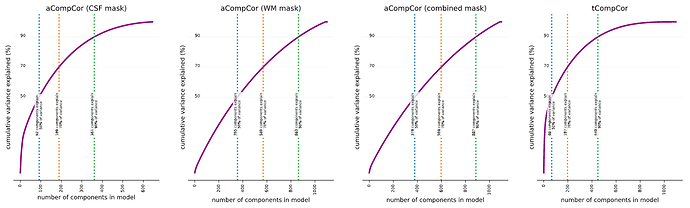
Could you elaborate on why the number of aCompCors (from either WM, CSF, or combined masks) should equal the number of TRs?
Fair question! The answer is baked in to PCA, a widespread but also complicated concept. I think that digging in to “what is PCA” a bit would clarify some of your other questions. Unfortunately, I don’t have a good go-to link/tutorial. Maybe this one https://blog.paperspace.com/dimension-reduction-with-principal-component-analysis/? Sticking with a neuroimaging resource, maybe this video from the principles of fmri? (Anyone else reading, please chime in with your own resources).
As a brief shot at an explanation, remember that PCA (on which aCompCor is based) is defined for any matrix. One of the (many) ways to think about a matrix is as a method for storing a collection of vectors. For example, each row could represent a different dimension, and each column a different vector (whether columns are dimensions or vectors will vary). If the matrix is 2 x 10, the matrix encodes ten points in a 2-d space. Of course, the first 2-d space we imagine has axes that are oriented vertically and horizontally, which means we can imagine the matrix as showing a regular scatter plot with ten points. But axes oriented horizontally and vertically are not always the most useful or the most concise. Consider the case of all ten points falling exactly on a line with slope 1. In that case, a more useful set of axes would be one that is rotated by 45 degrees, so that what was the horizontal x-axis lines up with the line. In PCA, we call the new axes ‘principal components’ (or special vectors / eigenvectors). With this new pair of axes, the points can be completely described by where they fall on just one of the components. The component along which all the points now fall explains 100% of the variance, so might as well drop the other!
In fMRI, the dimensions are timepoints, and each vector is a voxel. It’s essentially never the case that all ‘points’ fall exactly on a line (or other high-dimensional shape). Thinking back to the scatter plot, the points might be close to a line but with some variability around that line. This means that even after you’ve found a really good way to rotate the axes, you’ll still always need at least 2 dimensions (two coordinates) to specify the position of each point. One of those dimensions might explain more of the variability in the data, but you need both to get back to the original data (to store as much information as the original matrix).
Principal component analysis may be a bit of a misnomer. The analysis stops short of decomposing the given matrix into a set of components, each of which is assigned a relative importance. It’s up to the user to make the categorical judgement of which of these components are ‘principal enough’ to include in the subsequent analyses. The thing to remember is that each TR adds a new dimension, and each voxel included in the mask is another datum in that high-dimensional space. You’d need all components if you want a complete description of the original timecourse, which is why you get 1000 components when you have 1000 TRs. But often just a few can give a pretty good description of the activity in the masked region that is systematic.
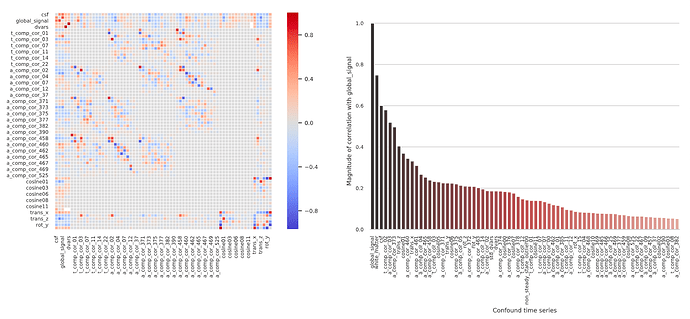
But it seems that if I include all aCompCors, it is using the aCompCors from the WM, CSF, and the combined mask?. Would this be redundant given that aCompCors from the combined mask contain information from both the WM and CSF masks?
The new docs that @oesteban linked starts to get at this. It’s not quite accurate to say that it would be redundant to include the combined mask if you’re included the WM and CSF mask, though the top components from all three likely explain similar sources of variance. The aCompCor components are calculated from each mask are calculated by running PCA with different combinations of voxels (e.g., only voxels in WM, only in CSF, or both). The best rotation that works for one set of voxels will tend not to be the same as the rotation that works for another set. e.g., imagine the scatter plot again where all ten points are on a line, but then an eleventh is way off the line. A rotation is only the ‘best’ when it enables all of the data to be concisely represented, so the best rotation will be slightly off the line with slope 1. The component that explains most of the variance will be like a regression line (still explaining a lot of the variance), with the second component still perpendicular to the first (explaining at least some of the variance). So you wouldn’t expect the top components calculated from the CSF and WM mask to necessarily match any of the top components from the combined mask (though they might be close). I’m not aware of any published, large/systematic assessment of aCompCor calculated with different masks. So if you test out different combinations, you may be in uncharted territory (which might be interesting, but likely warrants some validation).
I also had never seen so many aCompCors outputted
It’s my understanding that older versions of fmriprep only output the top 6 components (labeled 0-5), as calculated from the combined mask. I’m guessing that the reason to output only the top six was because Behzadi et al. consistently found that 6 components passed the broken stick threshold. But it seems at least plausible that the number of significant components depends on a bunch of factors (scan parameters, presence of artifacts, motion, etc), so at some point fmriprep started outputting more components calculated with different masks to give users more flexibility in subsequent analyses.
I’m aware that some tools exist to re-extract aCompCors from the unsmoothed AROMA-corrected data. But if I plan to use the smoothAROMAnonaggr output, I thnk I’d need to extract aCompCors from this file, not the unsmoothed file. Is this a correct interpretation?
I can’t comment much on the linked tools. But as a warning based on the link, the tool might not extract the principle components but instead the bold timecourses from each of these regions. If you wanted to run aCompCor, you’d then need to run your own PCA on those extracted timecourses.
hth
 . I’m sure others that search for info about aCompCors on neurostars will find that very helpful too.
. I’m sure others that search for info about aCompCors on neurostars will find that very helpful too.