Testing different noise models output from fmriprep - unclear results with ICA-AROMA

, , ,
1

Greetings,

I am testing the effects of various pre-processing “noise model” regressors (columns in the *_confounds.tsv from fmriprep) on rsfMRI connectivity’s association with motion (mean Framewise Displacement, in the *_confounds.tsv) on a dataset of ~325 young adults scanned on the same Prisma scanner. To do the noise model regression, I am using AFNI’s 3dTproject (in nipype), which affords simplicity in that it allows for regressing out “noise” time-series, censoring (…zeroing, or interpolating artifact TRs), regressing out trends, and smoothing. All denoising was conducted on the *_preproc.nii.gz output from fmriprep unless otherwise specified with an asterisk.

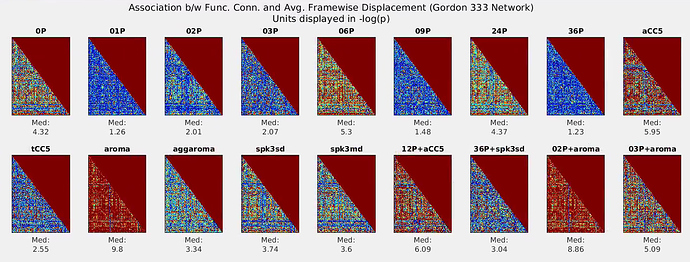
The noise models are defined below (* = uses the ICA-AROMA non-aggressive output)
0P = the “base” model (all other models contain these regressors): 6mm FWHM smoothing, first 5 TRs censored, 0th, 1st, and 2nd order detrending
1P = regression of GlobalSignal time-series
2P = regression of White Matter and CSF time-series
3P = 1P and 2P regressors
6P = regression of realignment parameters
9P = 3P and 6P regressors
24P = 6P regressors, their first derivatives, and quadratic terms of these
36P = 9P regressors, their first derivatives, and quadratic terms of these
aCC5 = aCompCor first 5 principal dimensions as regressors
tCC5 = tCompCor first 5 principal dimensions as regressors
aroma* = non-aggressive ICA-AROMA output, and 0P “base model”
aggaroma = “aggressive” ICA-AROMA regression conducted on 0P “base model”
spk3sd = spike regression
spk3md = spike regression, different threshold
12P+aCC5 = aCompCor5, 6P and their first derivatives (Chai et al., 2012)
36P+spk3sd = 36P and spike regression (Satterhwaite et al., 2013)
02P+aroma* = non-aggressive ICA-AROMA output, and 2P model regression (Pruim et al., 2015)
03P+aroma* = non-aggressive ICA-AROMA output, and 3P model regression (Burgess et al., 2016)

For each edge within a commonly used functional atlas (Gordon et al., 2016), I conducted linear regressions to examine the strength between functional connectivity strength (z-transformed temporal correlation coefficient) and subject movement in the scanner (mean Frame-wise Displacement output by fmriprep), and plotted absolute associations in the graphs below. Here, the association with motion is reflected in -log(p-value) and graph color scales range from -log(p=1.0) [blue] to -log(p=.0005) [red], so smaller/bluer values reflect less of an effect of motion (better). The median -log(p-value) is also presented below each graph.

56%20PM
Screen Shot 2018-08-30 at 2.21.56 PM.jpg1416×538 454 KB

My concern (and the reason for this posting) is that regression of some noise models seem to give especially poor results, particularly for when ICA-AROMA is used (see graphs labeled “aroma”, “02P+aroma”). The median association with motion is ~2x that of the 0P (“base model”). This is surprising to me, given that the number of “motion artifact” components identified by ICA-AROMA is typically much larger than even 36P. Overall, the full 36P regression had the least association with motion, but interestingly, a single Global Signal regressor seems to perform just as well.

I am curious if anyone has insight into this apparent disconnect in reasoning? Shouldn’t models that have regressed out more “motion”/“noise” variables as a result have less of an association with Frame-wise Displacement? Am I using the non-aggressive ICA-AROMA output correctly? Any suggestions would be helpful, as I have looked over my code a few times and cannot find any obvious mistakes.

Best,
Scott

3 Likes
2

It is indeed a surprising result. I’m not sure what could lead to such effect (although things each of these schemes is removing and measuring are related in non-trivial so way it is hard to form intuitions). Things that might be worth checking:

3

Not a comment on your results, but just a quick methodological note: I see you’re doing high-pass filtering through a 2nd order polynomial detrend. When we calculate a/tCompCor, we first high-pass filter with a discrete cosine basis (128s high-pass cutoff). We don’t save the high-pass filtered dataset, but we do save a copy of the basis in the CosineXX columns.

The intention was to use those in conjunction with CompCor detrending, if desired. I don’t really know what effect using these alongside a polynomial detrending would have; I suspect not much, but I don’t know if it would be significant when looking at these summaries.

4

Something seems strange here, adding in the motion parameters and their first derivatives into the aCompCor model made the correlation with FD stronger, which is strange since FD is just a linear combination of the motion parameters. Similarly, adding in the 6 motion parameters induces a higher correlation with FD than the base model.

I wonder if there’s any additional filtering steps and when they might be? I know that bandpassing just the BOLD data prior to regression actually induces artifacts and does a poor job accounting for the covariates.

5

Did you use a multiband sequence? We have found that aroma is not appropriate for such sequences.

6

Thank you all very much for the responses, @ChrisGorgolewski , @effigies , @jforawe , and @Alex_Fornito .

With regards to additional denoising/preprocessing steps taken before functional connectivity calculation, the 6mm FWHM smoothing took place only on data from the denoising schemes that used the *_space-MNI152NLin2009cAsym_preproc.nii.gz file, and no additional (i.e., second-pass) 6mm FWHM smoothing was done to the *_space-MNI152NLin2009cAsym_variant-smoothAROMAnonaggr_preproc.nii.gz file. A temporal band-pass filter was applied to each of the voxel-averaged time-series extracted from the Gordon et al., (2016) atlas; i.e., 0.009 to 0.080 Hz temporal filtering was conducted on voxel-averaged time-series, rather than single-voxel time-series (although I’m not sure I’d expect this to matter much).

The removal of 0th-, 1st-, and 2nd-order trends was conducted voxel-wise via 3dTproject, in the same step as the other noise regressors were removed. I did not use the CosineXX regressors, but I may give this a shot, especially for using the CompCor regressors. However, I am not certain it gets to the root of the problem, as other denoising schemes not using CompCor regressors (e.g., 6P or 24P, which only take into account the x, y, z, rotx, roty, rotz columns) inflate the association with Framewise Displacement relative to the base model.

@Alex_Fornito 's comment is interesting - the data are indeed collected using a multiband (factor = 4) sequence. Would you care to please elaborate? I have visually examined several of the *.html reports and found that AROMA seems to be tagging many motion-related components, but I have not looked at this quantitatively. Per @ChrisGorgolewski 's suggestion, I will have to look in more detail at the AROMA integration code, however, I have not implemented AROMA outside of fmriprep so I’m not sure I’ll have the keenest eye for potential problems.

One thing I noticed is that the columns of the *_confounds.tsv are not centered. While this would not explain the inflated FC<->FD association for the plain “aroma” scheme above, might it explain the increased FC<->FD association for other models? Should I be removing the mean of each column regressor (I thought this might’ve been done within the 3dTproject function, though)?

Also, has anyone else used AFNI’s 3dTproject to do denoising? I would be interested testing this out using other software (e.g., FSL) and a pointer to an easy (and ideally, fast, like 3dTproject) function would be helpful and greatly appreciated :slight_smile:

1 Like
7

I believe fsl_regfilt will do what you want, but I haven’t actually played with it.

1 Like
8

We found it gave unreliable results; ie run it twice on same data and get quite different results. we switched to fsl-fix and found that it does a very good job, provided you have 20 or so subjects and a bunch of time spare to establish a training set for your protocol!

4 Likes
9

Few months ago we did some simple comparisons of individual correlation matrices calculated on data obtained from fmriprep and SPM, and denoised in CONN toolbox and nilearn using confounds from fmriprep’s .tsv table. First, we noticed that correlation matrices from not denoised data (*_preproc.nii.gz) and output from ICA-AROMA (non-aggressive) were not very different in most cases. Second, when applying denoising (WM and CSF) on output from ICA-AROMA, histogram of correlation values was still little left skewed. For aCompCor we also included as confounds WM/CSF and 6 motion parameters. See example result attached. If I only find some more time, I will summarize this findings better.

example_cor_mat_comparison
example_cor_mat_comparison.jpg960×720 308 KB

I visually inspected output from fmriprep and ICA-AROMA results look fine.
We run fmriprep on data obtained on GE scanner, no multiband.

5 Likes
10

Thank you very much for sharing your results, @karofinc . Did you happen to correlate functional connectivity with an estimate of subject motion in the scanner (e.g., mean Framewise Displacement)?

1 Like
11

We didn’t, but I will do this together with summary of our findings. I should have it within two weeks. Thanks!

1 Like
12

This reminds me of a problem we have been working; see:

Later preprocessing steps can reintroduce previously removed artifacts if one isn’t careful. For example, temporal filtering after motion regression, can reintroduce the motion into the data. The amount depends on the interaction between the two filtering operations, not on the complexity of the motion regression. This could perhaps explain your findings.

6 Likes
13

Interesting observation @Alex_Fornito . I’m suspecting it will have to do with instability of the ICA decompositions. Are you limiting the dimensionality at all? We found it beneficial to limit the number of components to 100-150 for high volume multi-band data.

14

This was some time ago, so can’t remember off the top of my head. I don’t think we explicitly limited the #dimensions.

15

These might be helpful:
Figures 4-6 from https://www.sciencedirect.com/science/article/pii/S1053811917302288?via%3Dihub#ab0010

Figure 6 from https://academic.oup.com/cercor/article/27/9/4492/3056417#113569675

It really seems that the optimal preprocessing strategy may be dependent on the question that is being asked. When looking at individual or group differences it looks like using more motion parameters and scrubbing, or using ICA-AROMA (with our without GSR) may be reasonable bets. If anyone had other resources suggesting optimal preprocessing streams I would be all ears, particularly ones that synced nicely with fmriprep.

16

Thank you all for the feedback.

Thanks @mtnhuck , I modeled my preprocessing pipelines largely after the Ciric et al. (2017) paper, from what I understand, the approach I have taken differs very little from that of Ciric and colleagues. Yet, my results differ substantially. I am in the process of testing different software (i.e., FSL’s fsl_regfilt instead of AFNI’s 3dTproject for the regression) and will report back as soon as I have results.

Very interesting paper @fMRIstats , I will have to give a more detailed read to more deeply appreciate. Currently, I am using AFNI’s 3dTproject which I believe conducts a regression of nuisance variables (e.g., motion parameters), spikes (i.e., single TRs), and trends (0th, 1st, 2nd order) in one model. However, after extracting mean time-series for ROIs, I apply a temporal filter (butterworth, highpass = .009 Hz, lowpass = .080 Hz) in Matlab before computing temporal correlations. Does this seem to be problematic given your experience? In reading the abstract, it appears as though it might…

With regards to ICA approaches, ICA-AROMA does not seem to handle the “zebra-patterned multiband motion artifact” (e.g., see Figure 8 in Griffanti et al., 2017; https://www.sciencedirect.com/science/article/pii/S1053811916307583 ) that I see in some cases. I wonder if in your experience @Alex_Fornito , ICA-FIX can handle this in the classifier if given appropriate training data? Thanks for the suggestion @mmennes , I used the default component dimensionality selected in fmriprep, which may be a source of issue, but at a glance, for my data (TR = 1.5s, length = 400), the number of ICA components is seldom more than 150. Do you think this is too large of dimensionality? Is there a suggested way to check?

Thanks again all.

Scott

17

@burwell, my understanding is that if you use 3dTproject with the -passband flag specifying your bandpass range, it should simultaneously perform temporal filtering and nuisance regression, as recommended in paper by @fMRIstats. You do not need to do temporal filtering afterwards if you use that flag.

1 Like
18

its been a while, but in our experience it does pretty well.

1 Like
19

This is an interesting thread and I’m curious to hear what may explain the anomalous results…

I just wanted to mention that the use of 3dTproject will probably yield rather different results than fsl_regfilt given the ‘non-aggressive’ approach that the latter typically adopts. It’s also worth noting that ICA-AROMA has been vetted primarily using the non-aggressive method.

Briefly, the main difference is whether voxelwise BOLD data are regressed on noise components alone (this is what you’re doing with 3dTproject, I believe) versus regressed on all timecourses from the ICA decomposition (the non-aggressive fsl_regfilt approach). In the fsl_regfilt case, the partial regression coefficients reflect the association of a noise component with the data in the presence of both noise and ‘good’ components. The signal to be removed is computed by multiplying the partial coefficients for the noise components by the timecourses for those components, summing the results, then subtracting this from the BOLD timecourse.

Here’s a small R function that does the same thing as fsl_regfilt. y is a voxel timecourse, X is the time x components matrix from (melodic) ICA, and ivs is a vector of numeric positions in X containing flagged noise components.

partialLm <- function(y, X, ivs=NULL) {
  require(speedglm)
  #slower, but clearer to the math folks
  #bvals <- solve(t(X) %*% X) %*% t(X) %*% y
  #pred <- X[,ivs] %*% bvals[ivs]
  m <- speedlm.fit(y=y, X=X, intercept=FALSE)
  pred <- X[,ivs] %*% coef(m)[ivs]
  return(as.vector(y - pred))
}

This is a strong contrast to the 3dTproject approach where the association between noise and non-noise signal sources is not considered, which could lead to removal of potentially useful BOLD variation.

Hope this helps clarify at least one part of this anomaly.

6 Likes
20

Very nice explanation of what is going on. This approach divides the variance shared between noise and signal into the the noise and signal coefficients. In other words some, but not all and not none of the noise/signal shared variance will be removed from the data. How do you think this approach would compare to orthogonalizing the noise components against signal components prior to regression (in other words making sure none of the noise/signal shared variance is removed from the data)?