Hi neurostars,
We are using FSL’s randomise tool with the TFCE statistic and 5000 permutations to perform single-group-level inference on a group of model parameters [reference]. Everything was working like a charm, clusters were looking good, until I decided to explore a slightly different hypothesis using the magnitude of model parameters, regardless of sign. These are the results (in 1-p_value maps):
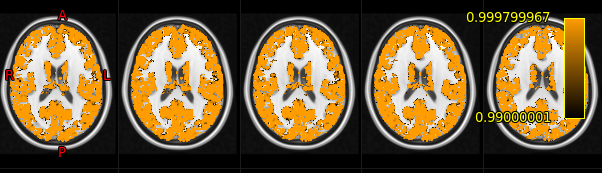
Everything turns out to be “significant”, which is obviously not what we were trying to do here: no greater TFCE statistic is ever found by chance anywhere. My guess is that permutations don’t actually flip signs at random, but rather interchange existing signs. So, since all signs are positive in my 4D data, permutations always end up looking like the original data (or something like that).
Is it possible (and correct) to tell randomise to do something like interchanging voxels spatially, so as to build the null model from spatial redistribution… or anything that will work for assesing significance of parameter magnitude? I don’t see any such option.
What would you recommend?
Thank you in advance,
Isaac
Summoning TFCE and randomise expert, @nicholst. I hope this doesn’t come across as rude.
@isacdaavid happy to be summoned! 
I need more information about what you mean by
until I decided to explore a slightly different hypothesis using the magnitude of model parameters, regardless of sign
In this do you mean you used a F-test?
Anyway, it is true that in a usual TFCE analysis based on a t contrast the TFCE sets all negative values to zero and the map is only assessing evidence for positive effects. Thus it is impossible to get an “all significant map” unless you have positive (and strong) values everywhere.
Now, for a F contrast corresponding to a single t-test, it is nothing but the square of the t-test. So while it is possible that an all-active map could be found it would be highly unlikely given that any time the original t map gets near zero the F map must get near zero and would be expected to break up the signal.
Finally, if this is a F contrast for 3 or more t-contrasts, if you have strong effects everywhere, it is indeed possible that you can get a ‘all significant’ map.
So, what I’m confused about is how you’re saying you’re doing “one-sample group inference” but then “testing the magnitude of all parameters”? Please be aware that “one sample group inference” only makes sense for testing input data that correspond to differences, i.e. where the mean under the null is zero. Perhaps you’ve input positive-only data? It then makes no sense to input into a one-sample t-test.
You need to ask yourself: At each voxel, what is the null hypothesis you’re testing on the input data. If they’re magnitudes, testing H0: mu=0 certainly isn’t interesting, but what is the interesting null?
-Tom
In this do you mean you used a F-test?
Neither t-maps nor F-maps. Input data are bare model parameters; actually not from GLMs, but SVM, which is why I can’t input test-statistic COPEs. SVM parameters are normally distributed (at the subject level) with mu=0, and comparison of TFCE maps between these (prior to testing this new wild idea) and regular GLM COPEs look pretty much the same, so I’m guessing I’m allowed to do this.
in a usual TFCE analysis based on a t contrast the TFCE sets all negative values to zero and the map is only assessing evidence for positive effects.
Ok. This explains why we need to perform fslmaths data.nii -mul -1 data-neg.nii for a 2-tail permutation test.
So, what I’m confused about is how you’re saying you’re doing “one-sample group inference” but then “testing the magnitude of all parameters”? Please be aware that “one sample group inference” only makes sense for testing input data that correspond to differences, i.e. where the mean under the null is zero.
You are absolutely right. Working with a different model made me forgot that the usual randomise input would be test statistics derived from GLM contrasts.
Perhaps you’ve input positive-only data?
Not at all. Let’s forget that these are not t-maps/F-maps for a moment. Suppose I have valid t-maps and I’m interested in measuring the probability that effects (positive and negative) will cluster at some anatomy. So I take the magnitude of the COPEs and use randomise with some form of cluster-informed inference to assign p-values to observations of cluster size/mass/etc., where H0 entails spatial interchangeability of magnitudes.
I’m afraid this is not how randomise flips data to estimate H0, right?
Errata: It seems that I have engaged in yet more inaccuracies in my previous comment. For the record, COPEs aren’t tstat maps themselves, but you can get tstats from the COPEs and VARCOPES following the definition of a t-value

