This is more out of curiosity and for learning than worry, but some folks have told me that I should investigate this further. I get the warning Note on orientation: qform matrix overwritten The qform has been copied from sform. in my .html report files for a dataset. From the discussion here, it seems like this usually shouldn’t be an issue, and is simply a warning. Is this indeed the case?
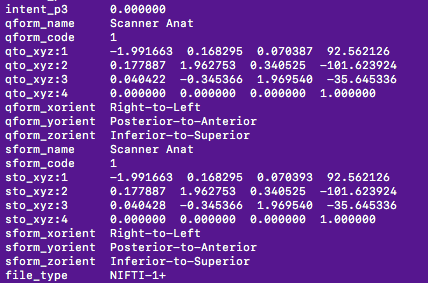
My curiosity came from visual inspection of the input files for FMRIPREP with fslhd, which yields that the qform and sform headers look exactly the same (at least to my human eyes, see below). What would yield this discrepancy? Is it decimal precision, or something? I see here that it’s probably due to not matching_affines.
Used fmriprep 1.2.5.
2 Likes
Looking at that, I agree that it shouldn’t be triggered. Perhaps we are overly-sensitive with our checks. Can you try, in Python:
import numpy as np
import nibabel as nb
img = nb.load(fname)
qform, qform_code = img.header.get_qform(coded=True)
sform, sform_code = img.header.get_sform(coded=True)
print("qform ({!s})\n{!s}".format(qform_code, qform))
print("sform ({!s})\n{!s}".format(sform_code, sform))
print("Equivalent:", np.allclose(qform, sform))
print("Maximum difference:", np.abs(qform - sform).max())
If this doesn’t indicate a difference, we have a logic error in there somewhere. If it does, it should tell us what threshold we would need to use in numpy.allclose to avoid a spurious warning.
2 Likes
That works! Looks like it is indeed a decimal precision thing, the output is below. I’m not sure if those differences are worth triggering the warning, as I’m not incredibly familiar with qform and sform, but it does seem like that’s what’s happening. Thanks for teaching me something along the way, too.
print("qform ({!s})\n{!s}".format(qform_code, qform))
qform (1)
[[-1.99166321e+00 1.68295321e-01 7.03872188e-02 9.25621262e+01]
[ 1.77886870e-01 1.96275293e+00 3.40524899e-01 -1.01623924e+02]
[ 4.04219863e-02 -3.45365936e-01 1.96954016e+00 -3.56453362e+01]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
>>> print("sform ({!s})\n{!s}".format(sform_code, sform))
sform (1)
[[-1.99166310e+00 1.68294877e-01 7.03930035e-02 9.25621262e+01]
[ 1.77887306e-01 1.96275294e+00 3.40524644e-01 -1.01623924e+02]
[ 4.04277816e-02 -3.45366180e-01 1.96954000e+00 -3.56453362e+01]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
>>> print("Equivalent:", np.allclose(qform, sform))
Equivalent: False
>>> print("Maximum difference:", np.abs(qform - sform).max())
Maximum difference: 5.795295573395032e-06
1 Like
To provide some context here, the qform and sform are 6 and 12 degrees-of-freedom alignment matrices. The qform is intended to encode scanner space, and the 6 DoF are 3D rotations and translations. The sform is intended to allow the same data to inhabit a second space, and this can be rotated, translated, scaled and sheared. The idea is that you could preserve the original data as retrieved by the scanner while still producing an alignment to another image, within the limitations of affine transformations. The standard specifies that if the sform is defined (has a non-zero sform_code), then it should be preferred to the qform for determining the alignment of the image, as it is more flexible and the result of analysis, while the qform is ostensibly written once at the initial NIfTI creation.
In practice, this dual-space use case almost never occurs, and practically nobody scales or shears their images without resampling. This means that there’s no advantage to permitting separate affine matrices, and also that almost all sforms can be copied into qforms with only some floating-point rounding errors.
Moreover, while most tools respect the sform, per the standard, ANTs in particular ignores it and strictly uses the qform. Therefore, because we want to mix and match transformations calculated by ANTs, FSL and FreeSurfer, it makes things dramatically simpler to make sure the transforms match.
So with all that said, I see a few options here:
- Relax the threshold for overwriting the qform. This would be easy, but we would need to be sure that transforms based on the qform (ANTs) and sform (everybody else) do not produce different results.
- Separate the overwrite threshold from the warning threshold. This would also be easy, but might be slightly deceptive, as somebody who actually did intend to use the two spaces might be surprised.
- Check whether the new qform is actually different from the old qform. If this 6e-6 difference is actually the rounding error from translating your particular affine matrix to quaternions, then we’re not changing anything, and the warning is deceptive, rather than overly cautious.
- Output the difference as part of the warning text, which would at least be more transparent. We could break it down into a rotational and translational difference, rather than a max.
Any thoughts?
cc @oesteban
1 Like
It seems like #3 and #4 make the most sense to me, although I’d obviously defer to folks with more expertise. However, I’m not sure how to check whether it’s actually rounding error (for #3). I know that the overwriting warning is generated for every one of my subjects–would it be helpful to check whether the magnitude of the difference between the qform and the sform is similar across all subjects?
That’s my feeling as well. I created this issue laying out a proposal for these changes: https://github.com/poldracklab/niworkflows/issues/361
To turn my proposal for checking for a rounding error into a quick test:
import numpy as np
import nibabel as nb
img = nb.load(fname)
hdr = img.header.copy()
qform, qform_code = hdr.get_qform(coded=True)
sform, sform_code = hdr.get_sform(coded=True)
hdr.set_qform(sform, sform_code)
new_qform = hdr.get_qform()
print("Equivalent:", np.allclose(qform, new_qform))
1 Like
On one subject, this test returns
print("Equivalent:", np.allclose(qform, new_qform)) Equivalent: True
I will try it on everyone and I will take a stab at addressing your proposal on github (although this is my first time trying such a thing, it seems very doable).
Sounds good. Let me know if you need any help getting started.
I ran into a complication–not all subjects return np.allclose(qform, new_qform)) Equivalent: True. I think this is because of the reliance in np.allclose on rtol * absolute(new_qform)), which differs in magnitude across different subjects? Unless this is indicative of a different problem, which is why I wanted to check in.
abs(sform-qform) still gives very small numbers for a subject that returns Equivalent: False. See below.
>>> print("Equivalent:", np.allclose(qform, new_qform))
Equivalent: False
>>> print("Maximum difference:", np.abs(qform - sform).max())
Maximum difference: 4.63360511006386e-05
>>> abs(sform-qform)
array([[3.17421826e-07, 3.71118277e-06, 4.63351030e-05, 0.00000000e+00],
[3.70080978e-06, 3.86374894e-08, 9.04311105e-07, 0.00000000e+00],
[4.63360511e-05, 8.64975704e-07, 4.18310195e-07, 0.00000000e+00],
[0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00]])
Edit: I think this is probably still fine if #2 in the proposal is addressed, since it would still yield a really small number.
Right. I think as long as people can see the diff and decide whether it’s expectedly big or expectedly small, we should be okay. The warning isn’t meant to indicate that something’s wrong, just that you might want to be aware of it.
1 Like
