Some question about second-Level fMRI Analysis in Nilearn: Design Matrix, Contrasts, and Parameter Clarification

[cfz]

Hello, I’m currently using Nilearn for the analysis of a within-subject fMRI study with a 2x5x2 design. I’ve encountered some issues during the second-level analysis and would greatly appreciate the insights from experts.

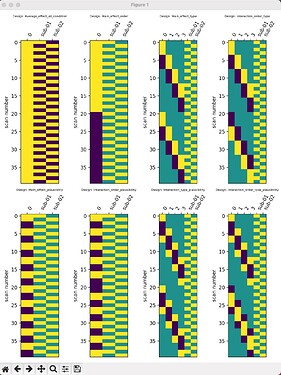
(1) In the first-level analysis, I extracted beta maps for each condition, resulting in 20 beta maps for each subject. The condition arrangement is as follows: A1B1C1, A1B1C2, A1B2C1, A1B2C2, A1B3C1, A1B3C2, A1B4C1, A1B4C2, A1B5C1, A1B5C2, A2B1C1, A2B1C2, A2B2C1, A2B2C2, A2B3C1, A2B3C2, A2B4C1, A2B4C2, A2B5C1, A2B5C2, where A represents the order, B represents the type, and C represents the plausibility. In the second-level analysis, I would like to obtain the main effects of A, B, and C, as well as their interactions. My current design matrix for the second-level analysis, which I generated based on the results from SPM’s function “spm_make_contrasts,” is shown in the figure below.

The contrast matrix was generated using the following code (based on https://en.wikibooks.org/wiki/SPM/Group_Analysis):

all_contrast_matrix = {
    'Average_effect_all_condition': [1]+[0]*n_subjects,
    'Main_effect_order': [1]+[0]*n_subjects,
    'Main_effect_type': [[1,0,0,0]+[0]*n_subjects,[0,1,0,0]+[0]*n_subjects,[0,0,1,0]+[0]*n_subjects,[0,0,0,1]+[0]*n_subjects],
    'Interaction_order_type':[[1,0,0,0]+[0]*n_subjects,[0,1,0,0]+[0]*n_subjects,[0,0,1,0]+[0]*n_subjects,[0,0,0,1]+[0]*n_subjects],
    'Main_effect_plausibility': [1]+[0]*n_subjects,
    'Interaction_order_plausibility': [1]+[0]*n_subjects,
    'Interaction_type_plausibility': [[1,0,0,0]+[0]*n_subjects,[0,1,0,0]+[0]*n_subjects,[0,0,1,0]+[0]*n_subjects,[0,0,0,1]+[0]*n_subjects],
    'Interaction_order_type_plausibility': [[1,0,0,0]+[0]*n_subjects,[0,1,0,0]+[0]*n_subjects,[0,0,1,0]+[0]*n_subjects,[0,0,0,1]+[0]*n_subjects],
}

Could you please confirm whether my design matrix and contrast matrix are correct for achieving my intended results?

(2) Additionally, there’s another within-subject condition D (task with 2 levels). Can I build on my current setup and perform another second-level analysis (effectively a third level) to incorporate condition D? This would allow me to investigate whether the observed effects change, disappear, or remain consistent across the different levels of D.

(3) I’m also unsure about the output_type parameter in nilearn.glm.first_level.FirstLevelModel.compute_contrast. How do ‘z_score’, ‘p_value’, and ‘effect_size’ differ, and why is ‘effect_size’ (i.e., beta) used in the first-level analysis and then fed into the second-level model? Is it possible to use ‘z_score’?

I’m relatively new to fMRI analysis, so please pardon the simplicity and naivety of my questions. I sincerely appreciate your assistance in advance!

[bthirion]

1. You need your design matrices not to be rank-deficient. This first one, for instance, is problematic. What you can do is remove one of the subjects columns. The others look fine AFAICT

2. Sounds OK, but you probably have to worry about multiple comparisons (you’re running more tests)

3. In general it is recommended to use effect size, because, you typically want to infer on the physical BOLD signal increase.
   If you want to use z-score, then you have to do it manually: obtain the z-score maps for each contrast you want to include in the second level analysis, and provide the list of these maps to a SecondLevelModel together with a design matrix. This should not be too hard…

HTH. Don’t hesitate to come back if you need more explanations.
Best,
Bertrand

[mica]

Hello !

@bthirion I’m facing a similar issue with my design matrix for my group analysis concerning the rank-deficiency. After my first level analysis, I have obtained one activation map per condition (A and B) for each subject. Now I want to look at the average/sum contrast between my conditions (i.e. A+B) taking into account the inter-subject variability. So I’m having something that is not too dissimilar to @cfz’s first matrix.

I was thinking of proceeding like you have mentioned in your previous answer (i.e. by removing one of the subjects columns), but I’m having some difficulty trying to understand how that could affect the interpretation of my results. Would it be possible to have more explanations about what it would mean ?

Thanks in advance for your time and help !

[bthirion]

If you want to do one-sample inference on A+B, but also want to have subject -specific regressors, you’re going to have no statistical power.
You want to infer on the population mean, so you need to include all subjects in the mean computation.
If you really want to disregard subject variability in the variance estimation, then you end up doing fixed-effects analysis.
Sorry if I misunderstood.
Bertrand

[m_p]

Thank you @bthirion for your answer !

Just trying to understand a bit better. Here’s the whole context: I have multiple conditions in my experimental paradigm and multiple runs per participant, let’s say A, B, C and D. I ultimately want to do a conjunction analysis on my 2nd maps, mainly the conjunction between the (A+B) map and the (D-C) map. I used nilearn for my first level and second level analysis. Here are the steps that I followed:

1- Compute my first level analysis to obtain my activation maps for each conditions for each participants (for each condition: I have one map per run per subject).
2- I computed the fixed effect using the compute_fixed_effect function in nilearn to obtain one map per condition per participant (based on this tutorial).
3- For my D-C map, I have created a design matrix including one column (D vs C) containing 0 and 1, and one column per participants (paired design; following this tutorial)
4- Now I want to proceed in a similar way for my A+B contrast. However, I can’t to exactly the same since in that case I have a rank-deficient matrix…

I’m not sure if it’s still possible to do what I want to do with nilearn or not. I’m a bit confused with the different steps. From what I read, it seems that I might want to do a random-effect model, but it’s quite unclear to me if that really solved my problem, and it that case how to proceed concretely.

Thank you a lot for your time, and patience !

[bthirion]

Indeed, you cannot remove the subject effect when you study the A+B contrast. The reason is that the subject effect is orthogonal to D-C, but it is colinear with A+B (indeed, the subject effect would fit the average of A and B, but this is actually what you want to measure: you cannot remove the effect you want to measure).
What you can do is thus to run the one-sample test on A+B and the paired t-test on C-D, and then do the conjunction.
Best,
Bertrand