Thank you very much for your informative comments @e.urunuela @handwerkerd !
First, I apologize for the length of this post—I wanted to thoroughly explore your suggestions before responding.
To address your initial questions: we are using a block design in our localizer task (3 runs), with 10 second category blocks being separated by 10 second fixation blocks. I don’t think our classifier can learn any shortcuts – we cross validate our accuracy results across 3 folds (train on run 1 and 2, test on 3; train on run 1 and 3, test on 2; etc.). Both the tedana and the no-tedana pipelines go through the same data split and seeds.
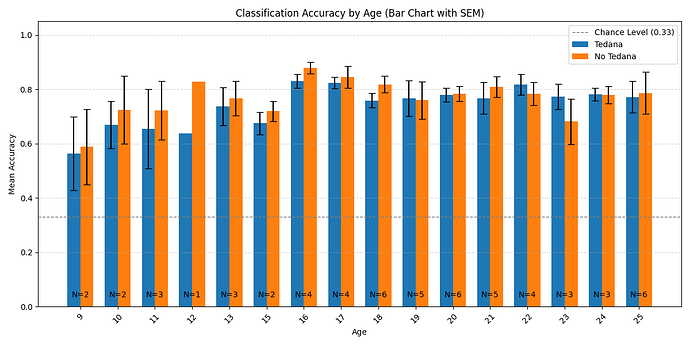
One thing I probably should have mentioned but didn’t in my original post, is that we are doing a developmental study (ages 8-25), thus our data includes children. After looking at the data more closely, what we ended up seeing was a suggestion that there is an age related effect on the difference in accuracy, which I previously overlooked.
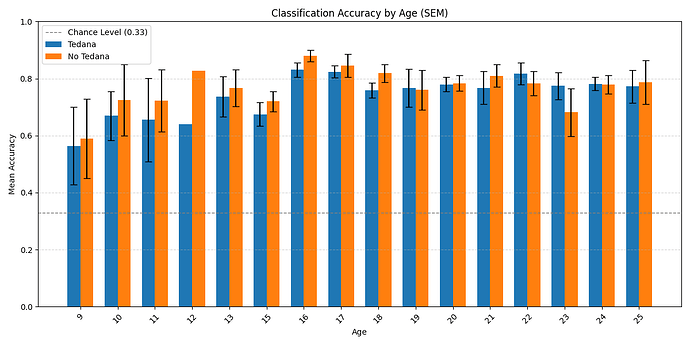
Here is the distribution of accuracy scores across ages:
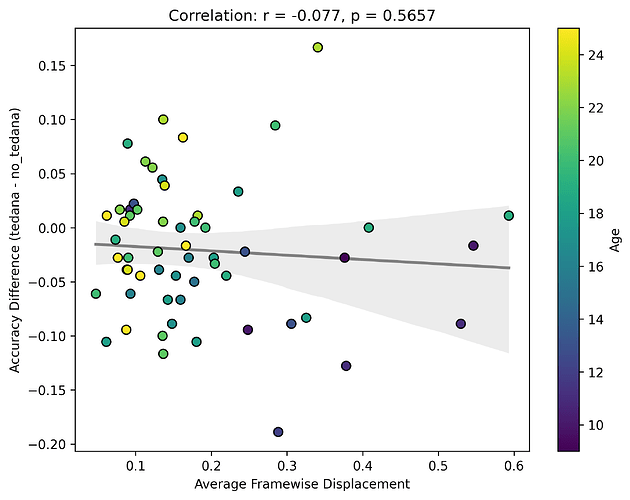
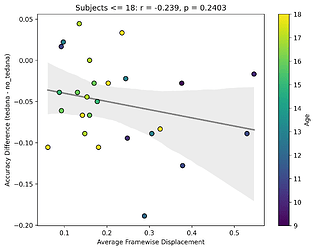
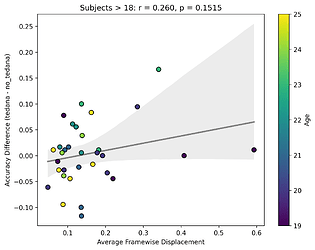
Looking closely you can see that tedana seems to consistently yield a lower accuracy in subjects aged 18 or less. We hypothesise this is due to children generally moving more in the scanner, so we ran a correlation between the subjects’ framewise displacements (average across all TRs of the 3 runs) and the accuracy difference, and found the following (FD vs Accuracy Difference):
N total: 59; N <= 18: 27; N > 18: 32
The correlations were not statistically significant, but aligned with the expected directions, at least for children. I think this might partially be due to the fact that we haven’t scanned enough children yet (especially aged 10 or lower), thus the effect is much weaker. In any case though, I guess it would be premature to say this is solely due to motion.
I ran a bunch of analyses correlating various statistics outputted by tedana with the difference between the tedana and no-tedana classifier accuracy, both at subject level and group level. Some of these analyses also suggested an age related effect.
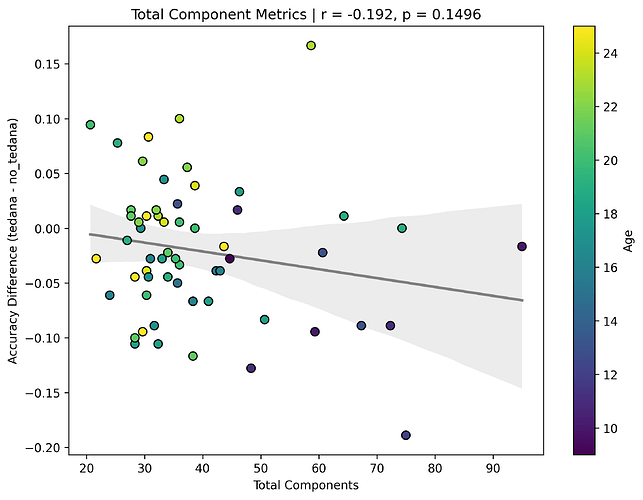
Firstly, it seems that the more components TEDPCA creates, the worse the difference becomes – and in general, more components are created in children. This effect is not significant, but to me it seems to be the main driver of the issues below:
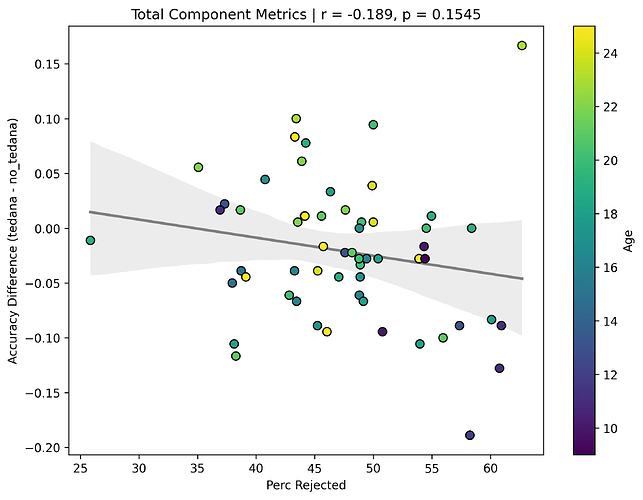
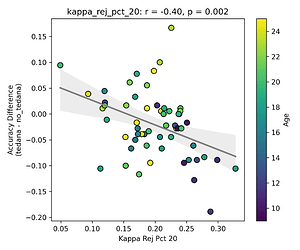
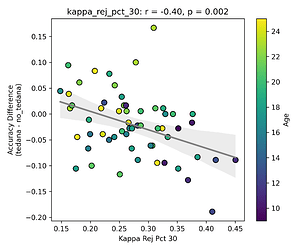
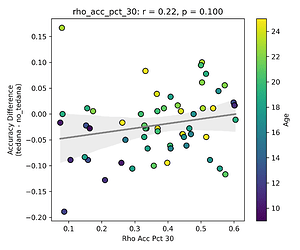
I then looked at percent accepted and percent rejected components (as opposed to raw values, since those would correlate with total amount of components created), and found that the bigger the proportion of rejected components is, the worse the difference – and kids seem to have a higher proportion of components being rejected. I’ll only attach the Percent Rejected vs Accuracy Difference plot here, since the percent accepted one would be identical but flipped.
Visually inspecting some subjects’ reports, I found that that the subjects that have more components close to the Rho/Kappa elbows seem to give worse accuracy. So I though I would look at the number of total, accepted, and rejected components within 10/20/30% of the kappa and rho elbow values (the range netween the actual value multiplied by 0.9 and 1.1, 0.8 and 1.2, and 0.7 and 1.3), and used those values as percentages of total components - I computed, for each run, the fraction of components rejected (or accepted) within 10/20/30% of the kappa and rho elbows, then averaged those run‑level percentages to yield a per‑subject mean percentage that we correlate against accuracy difference. I switched to percentages because raw “count within X% of the elbow” will naturally be higher in runs or subjects that simply have more components overall, whereas a percentage (run‑level count / total components, then averaged across runs) normalises for each run’s size.
Please excuse me if this is a naive way of doing this type of analysis, I wasn’t sure how else I could capture the influence of the elbow values. From my understanding, it seems to have an effect.
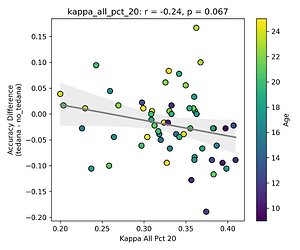
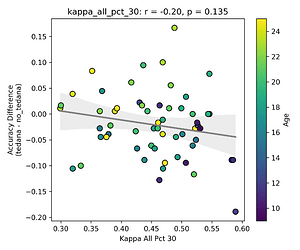
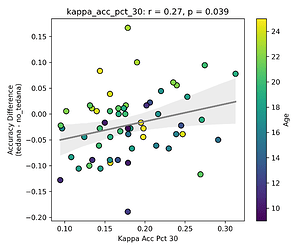
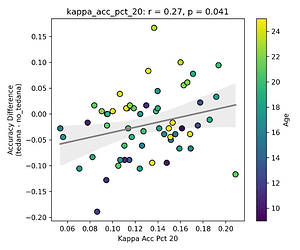
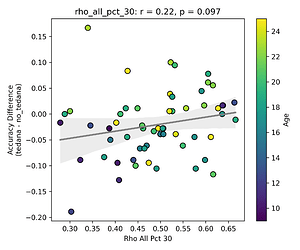
First, looking at values next to the kappa elbow – it seems that the more components are close to it, the worse the performance (no effect in within 10% of kappa value):
This effect is significant when looking at only the accepted/rejected components close to the kappa elbow:
The percentage of rejected components being close to the elbow appears to be age related.
I understand that a higher component kappa value = a higher likelihood of a component representing BOLD signal. What I assume this is implying is that some components laying close to the elbow do carry meaningful signal, but are still being rejected due to them not hitting a certain threshold (I know this is not only determined by how close a component is to the kappa elbow, but it seems to play a role in it?). So potentially tedana is rejecting too many components?
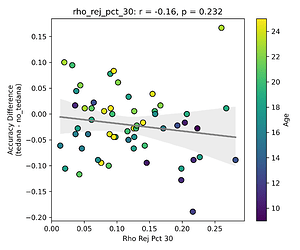
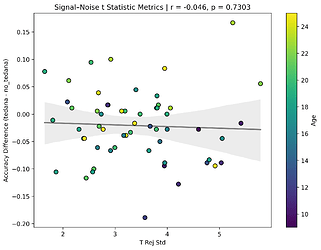
This effect is not as apparent while looking the same analysis done in regards to the rho elbow, and it is not significant. I’ll attach some only the most significant plots here (significance order is 30%, 20%, 10%).
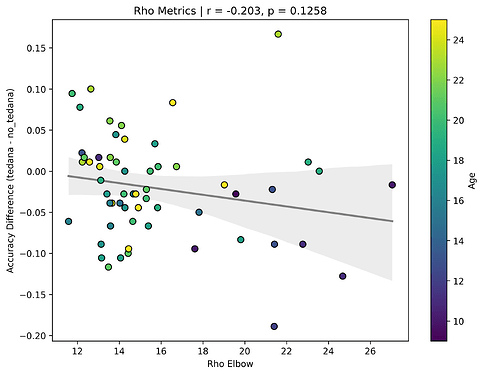
The actual rho elbow value seems to be lower in subjects with a worse accuracy difference (this is not the case for the kappa elbow value), and this seems to be age related:
Similarly to the above, since a higher row implies a lower likelihood of a component representing BOLD signal, and more rejected components close to it correlate to a worse classifier accuracy difference, tedana might be rejecting too many components below/close to the threshold? And if Rho elbow is lower, decision boundary shifts so more components fall in noise region?
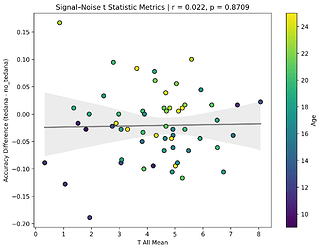
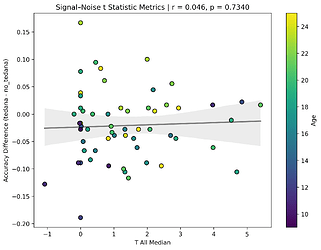
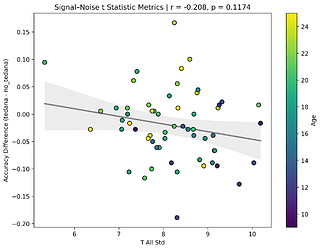
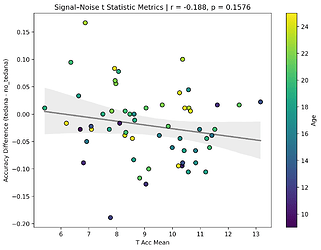
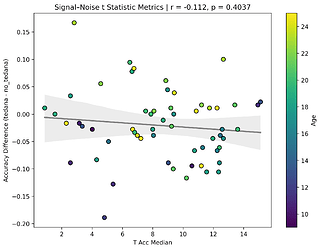
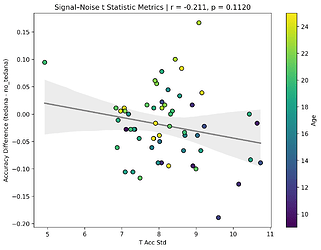
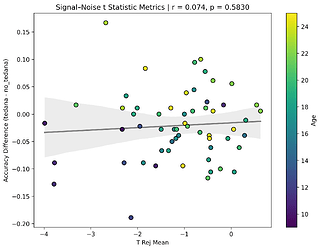
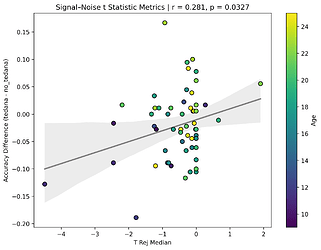
I also looked at the signal-noise_t of each component, calculated their mean, median, and std, and also correlated that, across total, accepted, and rejected components.
I’m not exactly sure how to interpret this. The stronger effects here seem to be driven by children’s data, who tend to have a lower median t-statistic for rejected components, and a higher t-statistic for accepted components.
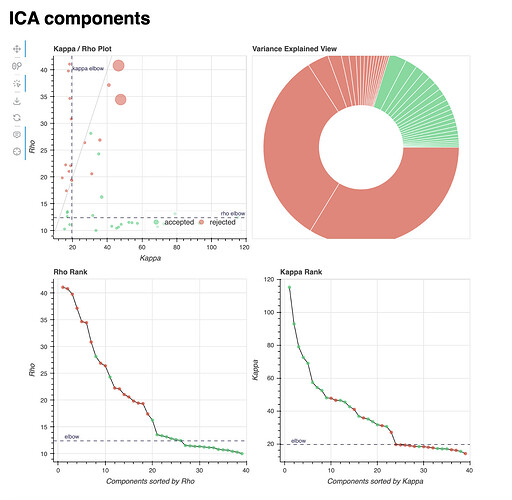
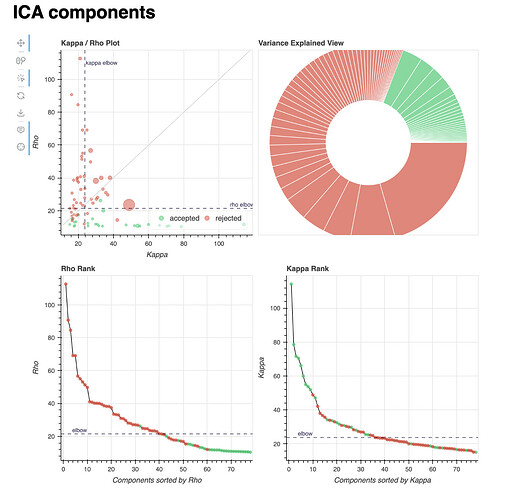
Lastly, I’ll add the component distribution of two example subjects: one showing a high classifier accuracy difference (84% vs. 74%, 10% difference, age = 23), and one showing a low one (64% vs. 83%, -19% difference, age = 12). These are the reports of a single localiser run, but all runs within each subject show a very similar distribution of components.
Subject with a higher tedana accuracy:
Subject with a lower tedana accuracy:
The component distributions in these subjects seem to concur with the broader analysis described above.
In light of these observations, is there a method within tedana to further reduce component rejection? Would you recommend we run manual classification of sorts – as in, reclassify N (or top N%) components closest to the elbow as accepted, and run denoising one more time? Would limiting the number of components PCA can create to a lower number be appropriate here? Maybe around 40-50, which would leave most subjects’ components unchanged.
Additionally, do you have any suggestions regarding running denoising on children’s data? Is there a standard way of implementing the tedana pipeline with children that you could refer me to?
Ultimately, we are trying to determine if tedana would provide an advantage for our analyses. We haven’t run any univariate analyses yet so it might be too early to say, but if using tedana requires extensive extensive manual adjustment, we aren’t sure whether the benefits would justify the additional complexity. Is there a point at which you would recommend we stop trying to make tedana work better, and stick to using the optimally combined data without any denoising?
Thank you very much in advance!! And again, very sorry for such a lengthy post.
Nikita