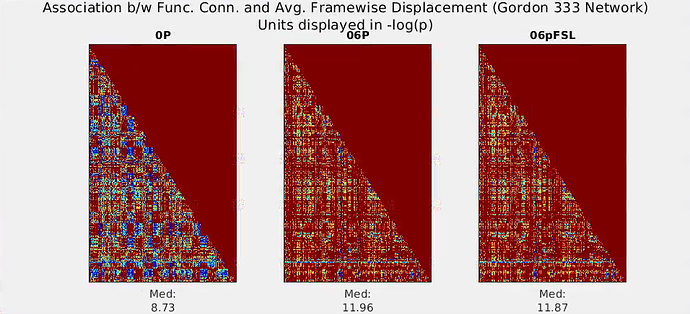
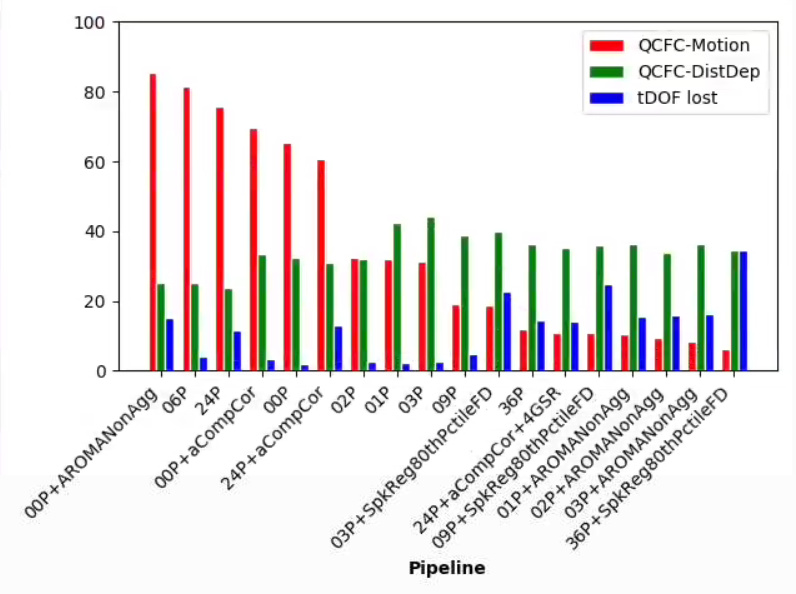
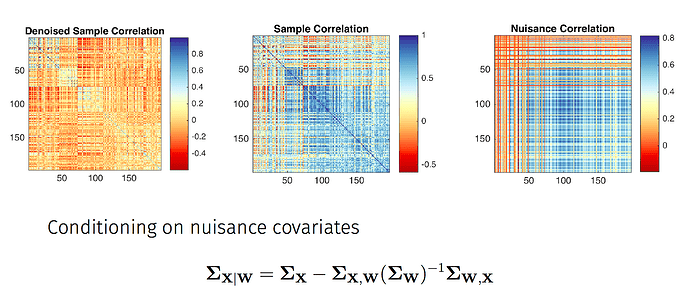
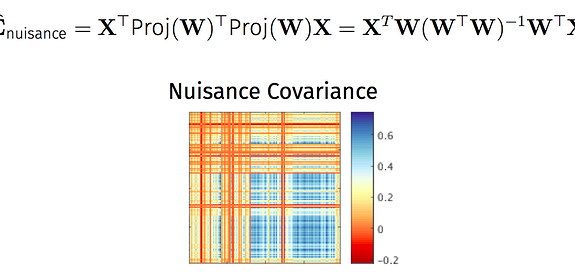
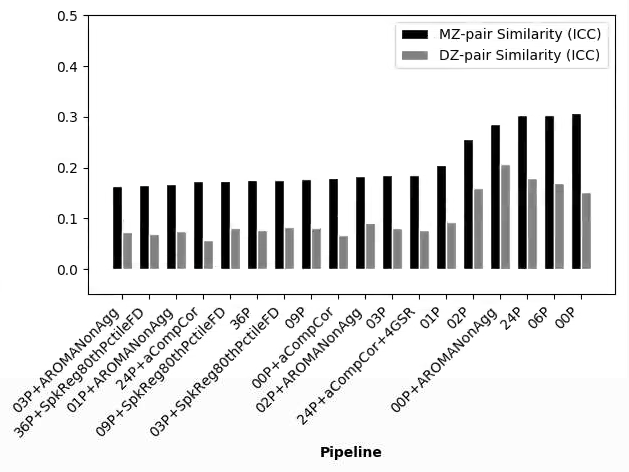
This is an interesting thread and I’m curious to hear what may explain the anomalous results…
I just wanted to mention that the use of 3dTproject will probably yield rather different results than fsl_regfilt given the ‘non-aggressive’ approach that the latter typically adopts. It’s also worth noting that ICA-AROMA has been vetted primarily using the non-aggressive method.
Briefly, the main difference is whether voxelwise BOLD data are regressed on noise components alone (this is what you’re doing with 3dTproject, I believe) versus regressed on all timecourses from the ICA decomposition (the non-aggressive fsl_regfilt approach). In the fsl_regfilt case, the partial regression coefficients reflect the association of a noise component with the data in the presence of both noise and ‘good’ components. The signal to be removed is computed by multiplying the partial coefficients for the noise components by the timecourses for those components, summing the results, then subtracting this from the BOLD timecourse.
Here’s a small R function that does the same thing as fsl_regfilt. y is a voxel timecourse, X is the time x components matrix from (melodic) ICA, and ivs is a vector of numeric positions in X containing flagged noise components.
partialLm <- function(y, X, ivs=NULL) {
require(speedglm)
#slower, but clearer to the math folks
#bvals <- solve(t(X) %*% X) %*% t(X) %*% y
#pred <- X[,ivs] %*% bvals[ivs]
m <- speedlm.fit(y=y, X=X, intercept=FALSE)
pred <- X[,ivs] %*% coef(m)[ivs]
return(as.vector(y - pred))
}
This is a strong contrast to the 3dTproject approach where the association between noise and non-noise signal sources is not considered, which could lead to removal of potentially useful BOLD variation.
Hope this helps clarify at least one part of this anomaly.
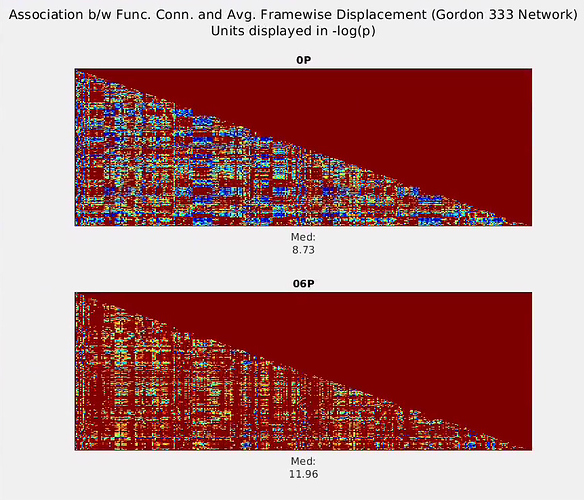
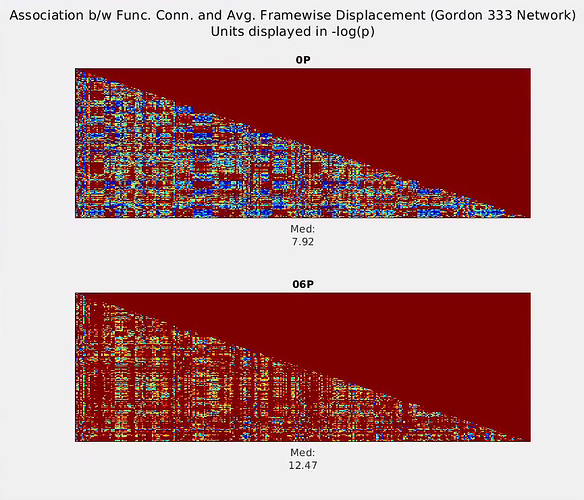
 ).
).