Here is the thread for W2D2 content discussion.
P.S. : Let me know if duplicate 
2 Likes
Hey,
thanks for starting this topic.
The Intro video doesnāt seem to introduce what linear systems are and the basic intuitions for the maths behind it (e.g. relationship between eigenvectors of the A mtx and dynamics, which is covered in 5s).
Does anyone know of a brief and effective intro to linear systems that the students could use to complement the intro video?
4 Likes
Just watched the intro vedio of W2D2. The moment I finished the vedio, I felt a great relief from chaos.
From my perspective, as a total beginner, I wish I could learn some basic information about linear system through a simple way. However, after the first several minutes, I was trapped in handwritten notions and complicated research without a good understanding of what we are talking about. I think W1D4 is good example.
3 Likes
cant agree more!!!
Have a look at the micro lectures in the tutorials? I felt they moved at a nice pace, and give some intuition about e.g. the relationship to the eigenvectors. Thereās also some references there for material you might want to watch in your own time
9 Likes
thanks, the videos in the tutorials are very helpful indeed.
I was hoping to find a primer to send my students to watch/read before the intro to help with understanding the intro itself.
I guess I can tell them to watch the first of the embedded videos.
The 3Blue1Brown videos are fantastic for algebra introductions (but they are quite abstract, so might be difficult for someone more application focussed to see the connection immediately)
1 Like
Hey,
This day actually incorporates several different topics (deterministic linear dynamical systems in continuous time and space, Markov processes, stochastic processes, auto-regressive models), each would have its own general introduction.
This course by the legendary Steven Strogatz is a great in-depth source for dynamics (despite its name, it starts with linear dynamics):
āhttps://www.youtube.com/playlist?list=PLbN57C5Zdl6j_qJA-pARJnKsmROzPnO9Vā
Lecture 1 is a nice overview, and lectures 2 and 5 cover deterministic linear dynamical systems in continuous time and space.
For something shorter and more concise, I guess the tutorial nano-talks would be a good resourceā¦
5 Likes
Thanks, that looks really interesting.
Iāll definitively have a look (though itās not a very concise primer for tomorrow 
)
Since weāre suggesting YT playlists, this great lectures series from Steve Brunton (related to teacher of W2D2 ?). Though the videos are mostly on control theory he goes in depth into linear systems and explains the topic with great clarity.
3 Likes
Yep, Steve and I have many collaborations, including 2 children 
His YouTube videos on dynamical systems are highly recommended, but Iām biased.
25 Likes
Perhaps the Intro video is not the most āIntroā materialā¦ The first Tutorial is trying to start from almost scratch and works through lots of the basics, although I do assume the students have been exposed to eigenvalues/eigendecompositions already (3blue1brown is strongly recommended).
4 Likes
The Intro video is very interesting, Iām just afraid it might not be accessible to students that havenāt seen linear systems before.
The tutorials videos and exercises are really great though, so Iām sure it wonāt be a problem and by the end of the day theyāll have mastered linear systems.
1 Like
Let me know how it goes!
Hey all, I think W2D2ās tutorials are very nice! Iām not too familiar with dynamics but I really enjoyed going through the notebook and the short videos. It was clear, at the right pace and spot on!
Just a quick note: in T4S1 the estimator of a in the OU process is unbiased. The reason you might see a systematic bias downwards might be due to using non-stationary data from the very beginning. If we instead estimate from data after, say, 100 time steps, and simulate for longer, the estimated a should converge to the true a pretty quickly!
1 Like
I second that. Eric did such an amazing job summarising a whole field of comp. neuro. research in 30mins, zero time wasted at all. But this would be a nice intro to someone more seniorā¦
So there is probably a casual short-handā¦? At around 5:48, they Taylor expansion should be around \bar{x}, but he did say verbally that this x is around \bar{x}.
4 Likes
Oh yeah, I also watched these and thought they were great! I was planning to recommend them for the Optimal Control dayā¦
2 Likes
If you have time at the end of Tutorial 1, you could try matrices A that produce stable/unstable spirals (eigenvalues that form a complex conjugate pair with a non-zero real part, for example A = [[-1, -2], [2, -2]] for a stable spiral and A = [[-1, -2], [2, 2]] for an unstable spiral, see below)
3 Likes
W2D2 tutorials are so beautifully done!
The only thing I could add as a bonus to tutorial 1 is a classification of equilibria that a linear system may have. Something like:
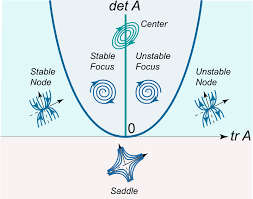
Sorry if I missed it somewhere.
10 Likes
Thatād be a wonderful addition as a bonus, initially I didnāt want to overwhelm even further with even more linear algebra.
2 Likes
A+ on trying these A matrices!